
Lethal and nonlethal chromosome aberrations by gamma rays and heavy ions: a cytogenetic perspective on dose fractionation in hadron radiotherapy
Introduction
Curvature in the biological dose response to ionizing radiation is arguably the most significant and widely studied of all radiobiological phenomena. It is inextricably linked to attenuated biological responses that accompany changes in radiation intensity, including: split-dose delivery, dose fractionation, and continuous low-dose-rate exposures, none of which occurs without an attendant display of curvature in the acute dose response. The general concept of curvature allows for low-dose/low dose-rate extrapolations in radiation protection (1), and has been the source of spirited debate pertaining to fundamental theories of radiation action (2-7). More to the topic of this paper, it forms the basis for understanding dose fractionation effects in radiotherapy, most notably in the context of mitigating late-developing normal tissue injury (8-11).
Curvature in the acute dose response portends a fractionation effect
Although typically associated with the so-called “shoulder” region of survival curves for mammalian cells exposed to X- or gamma rays (12), such curvature was actually first discovered and extensively investigated using cytogenetic endpoints (13,14). From these early studies of chromosome aberrations, core biophysical principles of time/dose relationships were developed that later formed the basis for more generalized theories of radiation action that are still used today (2). These core principles evolved from analyses of chromosome aberrations produced by low LET (linear energy transfer) X- or gamma rays, and eventually took the shape of the venerable linear-quadratic dose response relationship shown in Eq. [1], which relates the yield (Y) of aberrations to absorbed dose (D), and which may be considered characteristic of the cytogenetic damage response to all low LET radiations.
Not long after more exotic forms of ionizing radiations became available to investigators, it was discovered that the dose responses for radiations of much higher ionization densities (LET) lacked most or all of the curvature provided by the dose-squared term of Eq. [1]. For example, the dose response for low energy alpha particles could be described by the following simple linear function for the induction of chromosome aberrations.
From a radiobiological perspective, Eq. [2] can be considered an archetypal dose response to high LET radiation, for which the lack of curvature can be explained as follows. As the sole source of curvature in Eq. [1], the βD2 term represents a process involving the interaction of damage caused by multiple (independent) charged particle tracks. In the case of cytogenetic endpoints, the damage component of this process takes the form of initial radiogenic chromosome breaks. As originally envisioned, these breaks were scissions to the chromonema—the thread-like architecture of the interphase chromosome; in modern-day parlance the DNA double strand break would be substituted. The interaction component of the process takes the form of misrejoining between the broken ends liberated by such breaks, most likely via non-homologous end joining processes associated with DNA repair (15). Misrejoining leads to exchange-type aberrations (e.g., dicentrics, rings, translocations, inversions) which make up the lion’s share of chromosome aberrations produced by ionizing radiations. Classical cytogenetic theory asserts that the ability of broken ends to remain reactive (capable of misrejoining) decays with time, a process presumably attributable to DNA repair processes acting on these lesions. From a biophysical perspective, this forces the conclusion that for misrejoining to occur, the initial radiogenic breaks must be contemporary (close in both time and space). For acute dose responses, the time-based (temporal) component can be ignored, since the initial radiogenic damage produced by a charged particle track is practically instantaneous compared to the time scale for the cellular/molecular processing of lesions. In this way, one can appreciate that the βD2 term of Eq. [1] is inextricably linked to dose-rate/dose-fractionation effects, including both cell killing (16,17) and chromosome aberrations (18).
Presumptive linearity for high LET dose responses
Proximity of radiogenic breaks is an altogether different matter. Here, we refer to the physical distance between initial breaks, and the reactive ends thus produced. In this context, it should be appreciated that for most experimentally relevant doses of X- or gamma rays there are thousands of individual charged particle tracks traversing a cell. This allows for breaks produced by different (independent) particle tracks the opportunity to misrejoin. Often called the inter-track component, it is represented by the βD2 term of Eq. [1]. By contrast, the ionization densities of high LET radiations exceed those of x- or gamma ray by orders of magnitude, so equivalent doses would correspond to only a few tracks. The paucity of tracks severely limits the chances that breaks produced by independent tracks would be close enough to interact (misrejoin). The result is that virtually all such damage is limited to lesions produced along the same track, often referred to as the intra-track component. Consequently, the inter-track component responsible for curvature ceases to exist, and one is left with a linear dose response. Such is the case for low energy, high LET particles, like alpha particles from various naturally occurring radionuclides, which elicit dose responses described by Eq. [2].
In this paper we consider chromosome damage produced by a third type of ionizing radiation for which the characteristic dose response is not so well characterized—high-energy (HZE) ions, namely accelerated 56Fe ions. In terms of energy deposition, these particles simultaneously exhibit features normally attributed to both high- and low LET radiations. They are fundamentally high LET, in the sense that the “core” trajectory of their tracks is densely ionizing. On the other hand, their tracks are festooned with low LET secondary electrons (delta rays) that emanate radially from the track core. Importantly, as the velocity of such charged particles increases, a larger proportion of incident energy is imparted to delta rays which can traverse distances that take them well beyond the dimensions of a cell receiving the primary particle track. This is the situation for the 1 GeV/amu particles used in this study, where roughly half the energy is deposited by delta rays capable of traveling several cell diameters. In principle, this makes it more likely that interaction of damage produced by independent HZE particle tracks will occur. This was the explanation offered for the apparent curvature we observed previously for cytogenetic damage in response to these HZE ions (19).
Complex exchanges require rethinking of scoring criteria
Familiar terms like dicentrics, translocations, rings and inversions are easily definable, quantifiable, and intuitively understood for what they are—products of a misrejoining event involving exactly two initial breaks, distributed either between two chromosomes, or along a segment of the same chromosome. However, it is now widely appreciated that a sizable fraction of radiation-induced exchanges are complex, involving three (or more) initial breaks, distributed amongst two (or more) chromosomes. It is the “or more” aspect of this statement that requires us to adopt a more nuanced definition of cytogenetic damage. The problem with conventional classification schemes is that they fail to adequately convey the high level of complexity often seen for exchanges produced by ionizing radiation (20). This becomes evident when we consider complex exchanges involving the rejoining of more than three radiogenic breaks, which are relatively common, especially for high LET radiations (19,21,22). In this case, for example, it often becomes impossible (at any level of resolution) to determine whether a complex exchange involving four breaks is part of a single rejoining event, as compared to a combination of two independent simple rejoining events (20). That’s one issue. Another issue is that one intuitively judges a complex aberration involving, for example, six breaks and five chromosomes as being somehow more sinister to an intact genome than a simple pairwise exchange involving just two breaks on two chromosomes. This viewpoint seems defensible at the molecular level, when one considers that one of the more prominent mechanisms for chromosomally-derived carcinogenesis involves the illegitimate fusion of genetic elements between different chromosomes (23-26). On that basis, we argue that the number of illegitimate breakpoint junctions would be a more appropriate surrogate metric of carcinogenic potential than the number of underlying exchange events. The dose responses for these two measures of damage cannot be equivalent as long as the potential for complex exchanges exists (20).
Detecting curvature in dose response relationships
In a previous paper (27) we discussed strategies for detecting scant-to-moderate levels of curvature in the dose response of true simple chromosome interchanges to gamma rays. The objective of this study is similar; to determine whether such curvature exists for total breakpoints associated with chromosomal interchanges in human cells exposed to HZE 56Fe ions, and to discuss the possible relevance of our findings to radiotherapy. Detecting curvature following exposure to densely ionizing radiation (such as HZE particles) involves dealing with severe overdispersion in the underlying frequency distribution of chromosome damage within cells (28,29), prompting us to introduce customized information-theoretic methods of statistical analysis that are explained in the following section.
Here we seek to verify that upward dose response curvature (i.e., a positive second derivative) does, in fact, exist for total aberration breakpoints in the chromosomes of human cells exposed to 1 GeV/amu 56Fe ions (LET 150 keV/µm). Further, we ask to what extent the degree of curvature is affected when only surviving cells or, conversely, when clonogenically dead cells, are considered.
Methods
Cell culture and Irradiations
The procedures for 56Fe ion irradiations have been previously described in detail (30). Briefly, venous blood was obtained from a healthy volunteer following procedures approved by the Brookhaven National Laboratory (BNL) Institutional Review Board (IRB). Lymphocytes were isolated from this sample and suspended in RPMI-1640 medium (Gibco BRL, Grand Island, NY) supplemented with 20% fetal bovine serum (FBS). A 2-mL volume of this suspension was loaded into specially constructed Lucite holders at a concentration of approximately 106 cells/ml. These were exposed to 1 GeV/amu 56Fe ions at room temperature at the NASA Space Radiation Laboratory (NSRL) at BNL at a dose rate of approximately 1 Gy/min. The dose average LET for this beam was about 150 keV/µm. Immediately after exposure, cells were transferred to T25 tissue culture flasks containing 5 mL RPMI-1640 with 20% FBS and supplemented with 1% phytohaemagglutinin (PHA; Gibco). Cell cultures were allowed to grow at 37 °C for 46 h before Colcemid (0.2 µg/mL final concentration) was added 2 h prior to mitotic cell harvest. To abrogate the potential effects of mitotic delay following heavy ion irradiation addition, Calyculin (50 nM final concentration) was added to blocked cultures 45 min preceding harvest to induce premature chromosome condensation (PCC) in G2 phase cells. Thus, chromosome spreads from this experiment contain a mixture of G2 PCC and mitotic chromosomes. Harvested cells were fixed in 3:1 methanol to acetic acid by standard cytogenetic procedures and transported to the University of Texas Medical Branch (UTMB) at Galveston for analysis.
The procedure involving 137Cs gamma-irradiations has also been described (31). Lymphocytes were handled in a manner similar to that described above following methods approved by the UTMB IRB. Cells were irradiated using a J L Shepherd Mark 68-1 137Cs irradiator at a dose rate of 1.3 Gy/min at room temperature. Following irradiation, cells were incubated at 37 °C for 48 h as noted above. Three hours prior to harvest, Colcemid was (0.1 µg/mL) was added to each flask. Because significant cell cycle delay is not expected to alter the aberration yields following low LET exposures (32), Calyculin was not added to these cultures. Cells were fixed as described above.
mFISH analysis
In brief, cells were spread onto slides and chromosomal DNA was hybridized in situ to 10 µL of SpectraVision 24-color mFISH Assay probe (Vysis) as described in (31). Following a post hybridization wash, and DAPI counterstaining, images were captured using a Zeiss Axiophot epifluorescence microscope equipped with a black and white CCD camera. Image capturing, processing and karyotyping was accomplished using PowerGene image analysis software. The resulting karyotypes were analyzed following procedures earlier described and mPAINT descriptors were assigned to all aberrations (20). On the basis of these descriptors, cells were determined to be viable if they did not contain any asymmetrical exchanges or non-exchange (e.g., terminal deletions) aberrations.
Data sets for quantitative analysis
Using the aberration classification scheme described above, for each dose of gamma rays and Fe ions we generated frequency distributions of the number of breakpoints per cell in: (I) all cells; (II) only clonogenically viable cells (called “live cells” for convenience); (III) only clonogenically dead cells (called “dead cells” for convenience).
Dose response models
We assumed that the mean number of aberrations per cell (Y) at dose D could be described by either the linear-quadratic (LQ) model (Eq. [1]) or by the simpler linear (L) model (Eq. [2]). A comparison of statistical support for both models on the same data provides evidence for whether or not a curvilinear dose response is more consistent with the data than a linear one, and allows dose response curvature (the β parameter in Eq. [1]) to be quantified.
To deal with overdispersion (i.e., the variance is larger than the mean) which is known to occur in the probability distributions of chromosomal aberrations after densely-ionizing radiation exposure (28,29), we used the negative binomial (NB) distribution. This distribution is convenient for modeling positive integer count data, such as breakpoints per cell counts which we analyze here. For ease of interpretation, the NB distribution was parametrized as follows, where Y is the mean number of aberrations per cell at dose D predicted by either the LQ or L model, PNB(k) is the probability of observing k breakpoints in a cell, Γ is the Gamma function, and r is the “overdispersion” parameter:
PNB(k) = (1/[r × Q])1/r × (Y/Q)k × Γ(k+1/r)/[Γ(1/r) × k!],
Here, Γ is an extension of the factorial function, with its argument shifted down by 1. That is, if n is a positive integer: Γ (n) = (n-1)! Using this parametrization, the variance is described by the convenient expression Y + r Y2. Consequently, if r ~ 0, there is no overdispersion and the variance and mean are equal, as in the Poisson distribution. On the other hand, if r >0, then the variance becomes greater than the mean and the ratio of variance to mean increases as the mean increases.
For comparison, we also used the Poisson distribution, where the probability PPois(k) of observing k breakpoints in a cell is given by the following equation:
In summary, our dose response modeling approach consisted of two possible dose response shapes (LQ or L, Eqs. [1,2]) and two possible error distributions (NB or Poisson, Eqs. [3,4]). Each of these options was applied to data on gamma rays and Fe ions, which were in turn split into 3 subsets based on aberration classification: all cells, live cells only, and dead cells only. This resulted in 24 combinations of dose response model × error distribution × radiation type × aberration classification.
For each of these combinations, we fitted the appropriate model to the data by maximizing the log likelihood using the sequential quadratic programming (SQP) algorithm (33) implemented in Maple 2016® software. Uncertainties (95% confidence intervals, CIs) for each model parameter were estimated by profile likelihood (34).
Information theoretic model selection
We compared the statistical support for different model x error distribution combinations on the same data by using the Akaike information criterion with sample size correction (AICc), which has gained popularity for this purpose in various fields (35-37) including radiobiology. It takes into account sample size (the number of cells analyzed) and number of model parameters (which differs for the LQ and L models and for the NB and Poisson error distributions). The relative likelihood of the M-th model, called the evidence ratio (ERM), can be expressed as follows, where AICcmin is the lowest AICc value generated by the set of models being compared.
ERM = exp[−½ ∆AICcM], where ∆AICcM = AICcM − AICcmin
The normalized evidence ratio, i.e. the evidence ratio for the tested model divided by the sum of the evidence ratios for all the models being compared, is another useful quantity which is called the Akaike weight, AWM. It represents the probability that the M-th model would be considered the best-supported model (among those tested) upon repeated sampling of the data. The formula for the Akaike weight is:
AWM = ERM/∑MERM
Results
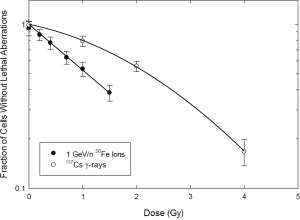
Figure 1 pertains to the killing of tumor cells within the high-dose/high-LET treatment volume. Here, a cell-by-cell assessment was made for metaphases, and only cells without presumptively lethal chromosome damage were considered. This included cells with no visible cytogenetic damage, as well as cells containing presumptively transmissible aberrations visible by mFISH, namely simple and complex translocations. The data are presented on a semi-log plot to emphasize the relationship to cell survival. Note the curvilinear/shouldered shape of the dose response for gamma rays, which is well fitted by the linear-quadratic model of survival, and which derives from Eq. [1]. In contrast, the “survival” response to 56Fe ions is apparently devoid of curvature, having a shape well-described as purely exponential.
As it pertains to secondary cancers from radiotherapy, we have argued that total exchange breakpoints are a better surrogate for carcinogenic potential than other measures of cytogenetic damage. Figure 2 shows the dose response for exchange breakpoints induced by 137Cs gamma rays compared to that produced by 1 GeV/amu 56Fe ions. The dose response for gamma rays shows the expected upward curvature characteristic of low LET radiations for various cytogenetic damage endpoints. Also as expected, the response to iron ions is much steeper. Rather uncharacteristically, however, there is seemingly slight curvature apparent in the dose response to the HZE iron ions. We were intrigued by the prospect of detecting such curvature, since it would imply a dose-fractionation effect for heavy ions. The curvature in question was slight enough that we sought to employ more sophisticated analytical/statistical methods in order to confirm its presence. The overdispersed nature of the distribution of breakpoints among cells for high LET radiations (38,39) prompted the rather rigorous analysis described in the Materials and Methods section.
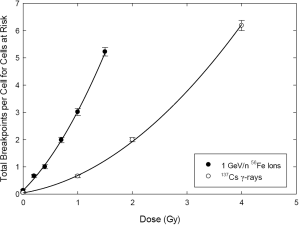
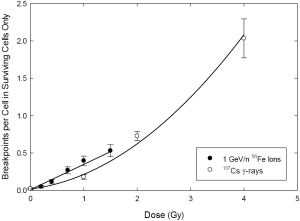
Figure 3 shows comparative dose responses for gamma rays and iron ions, wherein only cells devoid of presumptively-lethal aberrations are considered. In other words, cells containing asymmetrical chromosome aberrations (dicentrics, rings, terminal and interstitial deletions) were excluded from the analysis. As before, the response for total breakpoints shows the characteristic upward curvature for gamma rays. Interestingly, however, curvature is now even less apparent for the high LET 56Fe ions.
Our quantitative analyses of the dose responses shown in Figures 2 and 3 were consistent with visual inspection of these figures. For gamma rays, the “curved” LQ model with an NB error distribution was clearly preferred over all others: this preferred model had AW >0.97 on all data subsets (“all cells”, “live cells” and “dead cells”). The presence of overdispersion which resulted in higher support for the NB distribution rather than for the Poisson distribution (by >45 AICc units) was somewhat surprising for gamma ray data and may be a consequence of scoring breakpoints rather than exchange events.
For Fe ions, both the LQ and L models with NB error distributions achieved fairly similar statistical support (AW ranging from 0.32 to 0.69) for “all cells”, “live cells” and “dead cells”. Overdispersion (NB error distribution rather than Poisson) was strongly supported in each case (by >270 AICc units) and its magnitude (the best-fit value of parameter r and its 95% CIs) was larger than for gamma rays.
These results suggest that dose response curvature is strongly supported by the gamma ray data, whereas it is not clear (based on the data at hand) whether or not curvature exists in Fe ion data. In particular, curvature had the weakest support (the LQ model had the lowest AW of 0.315) in Fe-irradiated cells which contained only nonlethal aberrations. We have argued that the analysis of total breakpoints (instead of the exchange events themselves) should be the primary focus when considering second cancers. In this case, only those cells containing aberrations, but which are expected to survive, are important.
Discussion and conclusions
Hypofractionation presents undeniable potential benefits to patients. Among these are quality-of-life considerations associated with fewer hospital visits, and potential cost savings commensurate with a smaller number of delivered fractions. It is not our intent to weigh the relative merit of these factors against treatment outcome, but merely to address, in broad terms, the issue of hadron fractionation from a cytogenetic perspective, using a simple experimental model system.
Analogy to bona fide therapy beams
Ideal comparisons for our purposes would involve the measurement of chromosome damage by ~400 MeV/amu 12C ions in the plateau region of the track, versus the same ions in the Bragg Peak region. We are unaware of any such studies, and few cytogenetic laboratories even have access to hadron beams that would be considered relevant to radiotherapy (40,41). Fortunately, through our association with NASA, we had access to a 1 GeV/amu 56Fe beam line for these experiments. We rather doubt that these HZE ions would be considered for radiotherapy, mainly because the ratios of entrance/target doses are too high. However, their analysis may serve as theoretical guidance by evoking the following analogy. Consider, for example, 12C ions in relation to target volume. Entrance doses from such ions are of relatively low LET (~10 keV/µm). As such, their biological effects (e.g., cell killing) are not dissimilar to more familiar low LET radiations like protons, or the gamma rays used here (42). These effects would include curvature in the dose response relationship, and hence, tissue sparing from fractionated delivery.
In contrast, the LET of 14C ions (within the Bragg peak target volume) and the LET of HZE Fe ions used here (i.e., in track segment mode) are an order of magnitude higher. There are substantial differences in track structure between these ion species, such that the maximum range of the 1 GeV/amu 56Fe ions (used here) is far greater than that of therapeutic 14C ions at any point along their respective track-segment trajectories. Nevertheless, by comparison to the intended treatment volume, both ion species are well within the 100–200 keV/µm LET range of maximal biological effect, which is to say that the spread out Bragg peak (SOBP) for radiotherapeutic 12C ions and the plateau region of 1 GeV/amu 56Fe ions (used here) would have similar dose responses for cell killing (43,44). Additionally, and perhaps more to the point, neither dose response would be expected to exhibit curvature. It is by the analogy above that we consider 662 keV gamma rays and 1 GeV/amu 56Fe ions to be principally representative of the low-dose/low-LET entrance dose, and the high-dose/high LET target regions, respectively. To the extent that these analogies hold, we make the following observations in regard to hadron radiotherapy.
Tumor cell killing and asymmetrical chromosome aberrations
There is a strong and well-established relationship between chromosome aberrations and cell killing (45,46). If one assumes that asymmetrical aberrations (e.g., dicentrics and acentric fragments) are the main cause of reproductive cell death (32), it could be argued that they are, in some ways, superior to clonogenic measures of survival. For example, while it would be virtually impossible to distinguish 99% from 100% survival by standard clonogenic assays, finding a single aberration-bearing cell amongst 100 normals is a relatively routine affair. The same could be said when it comes to quantitative measures of curvature, as represented by the βD2 term of Eq. [1]. In context of this paper, it is not so much a 1:1 relationship between cell killing and chromosomal aberrations (32,45) that concerns us, but the shape of the dose response curves, as it relates to dose rate/dose fractionation effects (47). This would apply to tumor cells as well, although changes in ploidy and other conditions associated with a cancer phenotype are likely to complicate the relationship between aberrations and survival (48). While the objectives of this paper could be addressed using clonogenic survival (43,49-52) it could be argued that chromosome damage provides a more quantitatively robust endpoint. This is where the measurement of asymmetrical chromosome exchanges may find relevance to radiotherapy, where treating to the maximum dose allowable by normal tissue tolerance is likely the main dose-limiting consideration. Here the objective would be to maximize the number of tumor cells containing ≥1 asymmetrical aberration(s), while simultaneously minimalizing these events in normal cells. It would be, of course, the aim of hadron therapy to do this by limiting the physical dose (and dose equivalent) to normal tissue.
With reference to the weak support for dose response curvature for Fe ions shown in Figure 1 and by our quantitative analyses, fractionation in the high-dose/high LET (targeted) region becomes an irrelevant issue for tumor control, since it would have no material effect on survival. Conversely, the pronounced curvature associated with the dose response for gamma rays suggests that fractionation would lead to considerable sparing in normal tissues located proximal to the tumor, where the low-LET/plateau portion of the track occurs. Thus, from a cytogenetic perspective, we conclude that hypo-fractionation for heavier ion hadron therapy is a dubious proposition, as there is nothing to be gained in terms of killing tumor cells within the target volume. At the same time, it would effectively limit the total dose that could be safely given to the treatment volume, in order to avoid complications in normal tissues located in the proximal low LET/entrance portion of the beam.
Secondary cancers in normal tissue and symmetrical chromosome aberrations
To this point we have been discussing damage to normal cells in the context of cell death related to loss of organ function. Here we broaden the scope to consider another untoward consequence of radiotherapy, secondary cancers. Chromosomal damage is among the best surrogate measures of carcinogenic potential, where the concern centers on aberrations that do not kill cells, but which transmit to progeny. These would include the symmetrical types, namely reciprocal translocations (which mFISH readily detects) and inversions. It would also include complex exchange aberrations that involve three (or more) breakpoints, so long as the rearrangement is not associated with the formation of asymmetrical elements, because these produce acentric fragments.
This brings us to a discussion of Figure 3. For reasons that we do not fully understand, the slight apparent curvature for total breakpoints shown in Figure 2 became even weaker when we considered only those cells expected to survive. And yet, strong support for curvature persisted when a similar comparison between Figures 2 and 3 is made for gamma rays. Without getting into explanations that would take discussion beyond the intended scope of this paper, we suspect these results derive from the involvement of complex exchanges, since this is the main source of curvature seen in cells exposed to ionizing radiations (27,31).
Underlying mechanisms aside, the data shown in Figure 3 clearly indicate that there will be a pronounced fractionation effect for gamma photons, and (by our analogy) this will apply to cells exposed to therapeutic ions within the low-LET/entrance-dose region. However, if it is indeed the case that most secondary tumors are formed at the treatment margin of the high-LET/high-dose region (53), then only the small/negligible curvature seen for iron ions would apply. In this case, no substantial fractionation effect is expected for the induction of potentially carcinogenic chromosome aberrations. So, in the context of lowering the incidence of secondary tumors, fractionation is irrelevant to treatment strategy. In other words, the incidence of secondary cancers would be unaffected, irrespective of how the total dose is temporally apportioned.
Acknowledgments
Funding: This was work supported by the following grants from the National Aeronautics and Space Administration (NASA): NNX15AG74G (MC) and NNX14AC76G (BL).
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Marco Durante, Giusi I. Forte, Giorgio Russo) for the series “Radiobiological models towards a personalized radiation oncology” published in Translational Cancer Research. The article has undergone external peer review.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tcr.2017.05.16). The series “Radiobiological models towards a personalized radiation oncology” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). Approved by the Brookhaven National Laboratory (BNL) Institutional Review Board (IRB) #398, and the University of Texas Medical Branch (UTMB) IRB #99-145. Informed consent was obtained.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- National Research Council. Health Risks from Exposure to Low Levels of Ionizing Radiation: BEIR VII Phase 2. Washington, DC: The National Academies Press; 2006.
- Kellerer AM, Rossi HH. The theory of dual radiation action. Curr Top Radiat Res Q 1972;8:85-158.
- Kappos A, Pohlit W. A cybernetic model for radiation reactions in living cells. I. Sparsely-ionizing radiations; stationary cells. Int J Radiat Biol Relat Stud Phys Chem Med 1972;22:51-65. [Crossref]
- Goodhead DT. Saturable repair models of radiation action in mammalian cells. Radiation Research - Supplement 1985;8:S58-67. [Crossref] [PubMed]
- Tobias CA. The Repair-Misrepair Model in Radiobiology: Comparison to Other Models. Radiation Research Supplement 1985;8:S77-S95. [Crossref] [PubMed]
- Curtis SB. Lethal and Potentially Lethal Lesions Induced by Radiation --- A Unified Repair Model. Radiation Research 1986;106:252-70. [Crossref] [PubMed]
- Brenner DJ. Concerning the nature of the initial damage required for the production of radiation-induced exchange aberrations. Int J Radiat Biol Relat Stud Phys Chem Med 1987;52:805-9. [Crossref] [PubMed]
- Withers HR. Biologic basis for altered fractionation schemes. Cancer 1985;55:2086-95. [Crossref] [PubMed]
- Thames HD, Bentzen SM, Turesson I, et al. Time-dose factors in radiotherapy: a review of the human data. Radiotherapy and Oncology 1990;19:219-35. [Crossref] [PubMed]
- McBride WH, Withers HR. Biologic Basis of Radiation Therapy. In: Halperin EC, Perez CA, Wazer DE et al., editors. Perez and Brady's Principles and Practice of Radiation Oncology. 5th ed. Philadelphia: Lippincott, Williams & Wilkins; 2008.
- Zeman EM. The Biological Basis of Radiation Oncology. In: Gunderson LL, Tepper JE, editors. Clinical Radiation Oncology. 4th ed. Philadelphia: Saunders; 2016. p. 2-40.
- Puck TT. marcus P. Action of x-rays on mammalian cells. J Exp Med 1956;103:653-66. [Crossref] [PubMed]
- Lea DE. Actions of Radiations on Living Cells. London: Cambridge University Press; 1946.
- Lea DE, Catcheside DG. The mechanism of the induction by radiation of chromosome aberrations in Tradescantia. Journal of Genetics 1942;44:216-45. [Crossref]
- Richardson C, Jasin M. Frequent chromosomal translocations induced by DNA double-strand breaks. Nature 2000;405:697-700. [Crossref] [PubMed]
- Wells RL, Bedford JS. Dose-rate effects in mammalian cells. IV. Repairable and nonrepairable damage in noncycling C3H 10T 1/2 cells. Radiation Research 1983;94:105-34. [Crossref] [PubMed]
- Zeman EM, Bedford J. Dose fractionation effects in plateau-phase cultures of C3H 10T1/2 cells and their transformed counterparts. Radiat Res 1985;101:373-93. [Crossref] [PubMed]
- Cornforth MN, Bailey SM, Goodwin EH. Dose responses for chromosome aberrations produced in noncycling primary human fibroblasts by alpha particles, and by gamma rays delivered at sublimiting low dose rates. Radiation Research 2002;158:43-53. [Crossref] [PubMed]
- Loucas BD, Durante M, Bailey SM, et al. Chromosome damage in human cells by rays, particles and heavy ions: track interactions in basic dose-response relationships. Radiation Research 2013;179:9-20. [Crossref] [PubMed]
- Cornforth MN. Analyzing radiation-induced complex chromosome rearrangements by combinatorial painting. Radiation Research 2001;155:643-59. [Crossref] [PubMed]
- Anderson RM, Marsden SJ, Wright EG, et al. Complex chromosome aberrations in peripheral blood lymphocytes as a potential biomarker of exposure to high-LET alpha-particles. International Journal of Radiation Biology 2000;76:31-42. [Crossref] [PubMed]
- Anderson RM, Stevens DL, Goodhead DT. M-FISH analysis shows that complex chromosome aberrations induced by alpha -particle tracks are cumulative products of localized rearrangements. Proceedings of the National Academy of Sciences of the United States of America 2002;99:12167-72. [Crossref] [PubMed]
- Mitelman F, Johansson B, Mertens F. The impact of translocations and gene fusions on cancer causation. Nature Reviews Cancer 2007;7:233-45. [Crossref] [PubMed]
- Nowell PC. The minute chromosome (Phl) in chronic granulocytic leukemia. Blut 1962;8:65-6. [Crossref] [PubMed]
- Haluska FG, Finver S, Tsujimoto Y, et al. The t(8; 14) chromosomal translocation occurring in B-cell malignancies results from mistakes in V-D-J joining. Nature 1986;324:158-61. [Crossref] [PubMed]
- . Chromosome aberrations and cancer. Science 1991;254:1153-60. [Crossref] [PubMed]
- Shuryak I, Loucas BD, Cornforth MN. Seeking Beta: Experimental Considerations and Theoretical Implications Regarding the Detection of Curvature in Dose-Response Relationships for Chromosome Aberrations. Radiation Research 2017;187:7-19. [Crossref] [PubMed]
- Edwards AA, Lloyd DC, Purrott RJ. Radiation induced chromosome aberrations and the Poisson distribution. Radiat Environ Biophys 1979;16:89-100. [Crossref] [PubMed]
- Schmid E, Hieber L, Heinzmann U, et al. Analysis of chromosome aberrations in human peripheral lymphocytes induced by in vitro α-particle irradiation. Radiation and environmental biophysics 1996;35:179-84. [Crossref] [PubMed]
- Loucas BD, Durante M, Bailey SM, et al. Chromosome Damage in Human Cells by gamma Rays, alpha Particles and Heavy Ions: Track Interactions in Basic Dose-Response Relationships. Radiation Research 2013;179:9-20. [Crossref] [PubMed]
- Loucas BD, Cornforth MN. Complex chromosome exchanges induced by gamma rays in human lymphocytes: an mFISH study. Radiation Research 2001;155:660-71. [Crossref] [PubMed]
- Cornforth MN, Bedford JS. A quatitiative comparison of potentially lethal damage repair and the rejoining of interphase chromosome breaks in low passage normal human fibroblasts. Radiat Res 1987;111:385-405. [Crossref] [PubMed]
- Lawrence CT, Tits AL. A computationally efficient feasible sequential quadratic programming algorithm. Siam Journal on optimization 2001;11:1092-118. [Crossref]
- Venzon D, Moolgavkar S. A method for computing profile-likelihood-based confidence intervals. Applied Statistics 1988;87-94. [Crossref]
- Burnham KP, Anderson DR. Model selection and multi-model inference: a practical information-theoretic approach. Springer; 2002.
- Burnham KP, Anderson DR, Huyvaert KP. AIC model selection and multimodel inference in behavioral ecology: some background, observations, and comparisons. Behav Ecol Sociobiol 2011;65:23-35. [Crossref]
- McQuarrie ADR, Tsai C-L. Regression and time series model selection. Singapore; River Edge, N.J.: World Scientific; 1998.
- Ritter S, Nasonova E, Scholz M, et al. Comparison of chromosomal damage induced by X-rays and Ar ions with an LET of 1840 keV/mu m in G(1) V79 cells. Int J Radiat Biol 1996;69:155-66. [Crossref] [PubMed]
- Virsik RP, Harder D. Statistical Interpretation of the Overdispersed Distribution of Radiation-Induced Dicentric Chromosome Aberrations at High LET. Radiation Research 1981;85:13-23. [Crossref] [PubMed]
- Durante M, George K, Gialanella G, et al. Cytogenetic effects of high-energy iron ions: dependence on shielding thickness and material. Radiation Research 2005;164:571-6. [Crossref] [PubMed]
- George K, Durante M, Wu H, et al. In vivo and in vitro measurements of complex-type chromosomal exchanges induced by heavy ions. Advances in Space Research 2003;31:1525-35. [Crossref] [PubMed]
- Yang H, Anzenberg V, Held KD. Effects of heavy ions and energetic protons on normal human fibroblasts. Radiatsionnaia Biologiia, Radioecologiia 2007;47:302-6. [PubMed]
- Blakely EA. Cell inactivation by heavy charged particles. Radiation & Environmental Biophysics 1992;31:181-96. [Crossref] [PubMed]
- Takiguchi Y, Miyamoto T, Nagao K, et al. Assessment of the homogeneous efficacy of carbon ions in the spread-out Bragg peak for human lung cancer cell lines. Radiation Medicine 2007;25:272-7. [Crossref] [PubMed]
- Revell SH. Relationship between chromosome damage and cell death. In: Ishihara T, Sasaki MS, editors. Radiation-induced chromosome damage in man. New York: Liss; 1983. p. 215-33.
- Cornforth MN, Bedford JS. Ionizing radiation damage and its early devlopment in chromosomes. Adv Radiat Biol 1993;17:423-96. [Crossref]
- Bedford JS, Cornforth MN. Relationship between the recovery from sublethal X-ray damage and the rejoining of chromosome breaks in normal human fibroblasts. Radiation Research 1987;111:406-23. [Crossref] [PubMed]
- Schwartz JL, Murnane J, Weichselbaum RR. The contribution of DNA ploidy to radiation sensitivity in human tumour cell lines. British Journal of Cancer 1999;79:744-7. [Crossref] [PubMed]
- Fujisawa H, Genik PC, Kitamura H, et al. Comparison of human chordoma cell-kill for 290 MeV/n carbon ions versus 70 MeV protons in vitro. Radiation Oncology 2013;8:91. [Crossref] [PubMed]
- Blakely EA, Chang PY. Biology of charged particles. Cancer J 2009;15:271-84. [Crossref] [PubMed]
- Raju MR, Bain E, Carpenter SG, et al. A heavy particle comparative study. Part II: cell survival versus depth. British Journal of Radiology 1978;51:704-11. [Crossref] [PubMed]
- Oonishi K, Cui X, Hirakawa H, et al. Different effects of carbon ion beams and X-rays on clonogenic survival and DNA repair in human pancreatic cancer stem-like cells. Radiotherapy & Oncology 2012;105:258-65. [Crossref] [PubMed]
- Newhauser WD, Durante M. Assessing the risk of second malignancies after modern radiotherapy. Nature Reviews Cancer 2011;11:438-48. [Crossref] [PubMed]


