Nuclear interactions of new ions in cancer therapy: impact on dosimetry
Introduction
Radiotherapy with ions has come a long way since its beginning at the Lawrence Berkeley Laboratory (LBL) (Berkeley, CA, USA) in 1954. The pioneering work accomplished there set the ground for an unexplored but yet promising approach to tumor treatment and opened new perspectives in the field. Today, charged particle therapy (CPT) is a well-established strategy against cancer and its combination with surgery and chemotherapy is becoming a standard for most cases.
LBL’s experience with heavy ions started about twenty years later than protons and until 1993, when the Bevalac facility was shutdown, almost 3,000 patients received treatments mainly with beams of 4He and 20Ne but also with 12C and 40Ar ions. Encouraged by this work, Japan built the Heavy-Ion Medical Accelerator (HIMAC) at the National Institute of Radiological Sciences (NIRS) in Chiba (Japan), and became operational in 1994, electing to use 12C ions as the standard radiation. At the same time a new delivery solution (the scanning technique), which differs significantly from the previous approach used at the LBL and HIMAC, was developed at the Helmholtz Center for Heavy Ion Research (GSI) in Darmstadt (Germany) using Carbon ions and at the Paul Scherrer Institute (PSI) in Villigen (Switzerland) using protons. Today, there are over fifties proton therapy centers and ten 12C ions facilities operating in the world (1). Following this trend, scientists focused on establishing, tuning and optimizing the treatment procedure for Carbon beams and protons only and the use of other ions was overshadowed. However, once the community gained knowledge and confidence in this methodology, it has started to open up to new challenges and once again has begun exploring the possibility to perform radiotherapy with other ions.
Based on the physics and radiological data so far collected, people abandoned the idea of finding the “optimal particle” for curing cancer and instead has been more inclined to an approach where the selection is done case-by-case out of a pool of possible candidates ions.
The concern for induced secondary malignancies when using Carbon ions on pediatric patients (2) has led to look for a lighter alternative. Physics, biology and nuclear interactions of new ions in cancer therapy for clinical data collected in Berkeley for over 2,000 cases pointed to Helium as the most attractive particle.
On the other hand, the rationale for choosing an ion heavier than Carbon is to overcome the radioresistance of very hypoxic tumors by using a higher linear energy transfer (LET) radiation (3,4). The best candidate for this application is Oxygen, which has also the advantage of reducing the oxygen enhancement ratio (OER) (5-7).
On the basis of these considerations, several heavy ions centers have been designed with the capability to deliver also 4He and 16O ions with energies in the therapy range. For example, both species are already available at Heidelberg Ion-Beam Therapy Center (HIT) (Heidelberg, Germany) for research purposes.
An overview of the physical advantages and disadvantages of Helium and Oxygen ions and their comparison with protons and Carbon ions is presented in this review. The nuclear interactions of interest are illustrated together with the theoretical approaches proposed for modeling them. The work also outlines the experimental data available in literature for the characterization of these reaction processes and illustrates how they influence the beam physical dosimetry in terms of depth dose and lateral profiles. The considerations highlighted by the study will be the platform for developing a wider discussion, where also radiobiological and clinical points of view are taken into account.
Nuclear interactions
When a new ion has to be implemented in a treatment planning system (TPS), the following physical processes have to be characterized and modeled: production of secondary fragments from nuclear interactions, energy loss and lateral scattering of primary and secondary ions. These interactions modify the primary radiation composition, energy and direction and thus influence its depth dose and lateral profile.
Coulomb repulsions between the ion and the target nucleus cause a lateral diffusion of the primary beam and can be described with the Multiple Coulomb Scattering (MCS) theory proposed by Molière (8). The physical bases of this approach have been extensively presented in several books and reviews (9-11) and thus will not be discussed here.
Fragmentation is caused by nucleus-nucleus interactions via strong nuclear forces and the most popular approach for its modeling is the abrasion-ablation (or cascade- evaporation) theory. It is based on a two-steps process and fully describe the peripheral collisions of the projectile with the target nucleus adopting a geometrical approach. This model has been accurately illustrated in several works (12-16).
In both stages, projectile and target fragments can be created but they have pretty different characteristics in terms of species, energy and angular distribution.
In the abrasion step, projectile fragments (pre-fragment) retain almost the same velocity and direction of the projectile (vf ≈ vp) and approximately the same ratio of mass over nuclear charge (A/Z)f ≈ (A/Z)p. The fragments momentum changes are well reproduced by Goldhaber’s theory (17) and an accurate illustration can be found in (18). The excitation energy gained in the abrasion process can be described with two theories proposed by Hüfner et al. (14) and Glauber et al. (13,15). The former is based on the liquid drop model and the surface tension is responsible for the excitation energy if the nuclear structure is changed. The second theory, instead, relates the excitation energy of the pre-fragment to the creation of vacancies in the Fermi distribution. When the projectile is in its ground state, the nucleons move in the appropriate nuclear potential well according to the Fermi gas model. When a number of nucleons are removed from the projectile, the wave functions of the remaining nucleons are only slightly disturbed by the abrasion, meaning that they will not adapt themselves to the deformation. Therefore, the only consequence of the collision is the creation of vacancies in the potential well. The excitation energy is then given by the sum of the energies generated by the creation of these holes with the respect the Fermi surface.
In the ablation phase, instead, (A/Z)f is smaller than (A/Z)p and the nuclear de-exitation (or evaporation process) occurs through decay to the ground state by emission of neutrons, protons and light nuclei as well as by fission and emission of γ-rays. During the whole de-excitation phase there is a competition between these different processes and in general this stage is described by numerical statistical model, where the probability to create a fragment from the pre-fragment decay depends on the excitation energy gained in the abrasion step. Statistical model for the ablation phase have been elegantly formulated by Campi and Hüfner (16).
In all these processes, projectile fragments have a kinetic energy spectrum peaked at the same energy of the primary beam and they are mostly emitted in the forward direction (19-22). Moreover, light secondary fragments, like protons and neutrons, show tails in the kinetic energy spectra up to twice the primary beam energy. This is possible because of the Fermi momentum transferred from the nucleons of the target nuclei. Nucleons inside the nuclei follow the Fermi gas model and move with a momentum of ~250 MeV/c (23).
Target fragments, originated either through direct abrasion in the collision with the beam particles or from evaporation in the ablation stage, are emitted isotropically in the rest frame of the target (and to a good approximation also the laboratory frame). As the target nucleus is at rest before the collisions, its fragments have a much lower energy than those created by the projectile. Furthermore, particles with Z higher than the primary beam can be produced through this process. Target fragmentation creates high-LET secondaries, whose value can exceed that of the primary ions especially for light beams like protons and Helium.
For clarity, the definition of the different type of cross section mentioned in this work are reported below. The total reaction cross section (σr) refers to the probability of all the possible nuclear reaction channels in the interaction of the ion with the target material via nuclear forces. The total charge-changing cross section (σtcc) is related to the probability for a primary ion to change its charge but not its mass. The probability to produce a fragment with different charge (Z) from the projectile is called partial charge-changing cross section (σpcc). If the fragment type can be identified not only in Z but also in mass (A), the associated cross section is referred to as total fragmentation cross section (σtf). Double differential cross sections are related to the probability of producing a fragment species at a certain angle and with a given kinetic energy.
For beams above ~1 GeV/u, the total reaction cross section is independent of the projectile energy and equal to a geometrical cross section expressed by the Bradt-Peters formula (24)
σr = πr02(A1/3+ A1/3− c)2
where AT and AP are the mass of the target and the projectile, respectively, c is the overlap transparency parameter and r0 is 1.1 fm. From the latter, the geometrical nuclear radius can be calculated as r = r0A1/3. This approach becomes less accurate in the therapeutic energy range, where all total reaction cross sections are energy-dependent. For this reason, several corrections were added to the Bradt-Peters formula and have been presented and discussed elsewhere (9,25). This theory describes well the interactions of heavy ions with matter and is very suitable for modeling 12C and 16O ions in radiotherapy.
For proton beams, instead, no projectile fragmentation occurs and the abrasion-ablation theory has to be replaced by a one-step approach for modeling target fragmentation. Protons can interact elastically or inelastically with the target nuclei (26). In the former, the target nucleus remains in its ground state with a recoil kinetic energy pretty small so that the scattered proton will have nearly the same velocity as prior the impact. This type of collision can be described with an optical potential model (26). When inelastic scattering occurs, instead, there is high momentum transfer. The proton is scattered at a large angle and the target nucleus is left in an excited state (26). When protons interact directly with the target nucleons, reactions of knockout and pickup take place.
One-step direct reactions, like the one mentioned above, reproduce well also nuclear interactions of 4He ions with matter (27). In this approach, the fragmentation channels are produced by processes of stripping, pickup, knockout and total break up where the projectile may lose energy or have one or more nucleons transferred to the target or removed. Fragments production of 4He ions on a target nucleus is a simpler mechanism than for heavier ions (as 12C or 16O) due to the limited combinations of possible final states. The reaction channels for these processes are:
where X is the final target stage (27). The reaction channel 4He+A → n+n+p+p+X shows a complete breakup of the Helium nucleus. This would lead to a more than three body dissociation process and an example it is given by the reaction p+4He → p+p+p+n+n. A phenomenological approach for calculating the cross sections related to the production of different fragment types (3He, deuterons and tritons) was proposed by Cucinotta et al. (27) with the following formalism:
where T is the projectile energy in MeV/u and Tth the energy threshold in MeV of the single reaction channels. The cross section of the pickup process is defined as
Combining Eqs. [3] and [4], the 1H production cross section is then calculated as
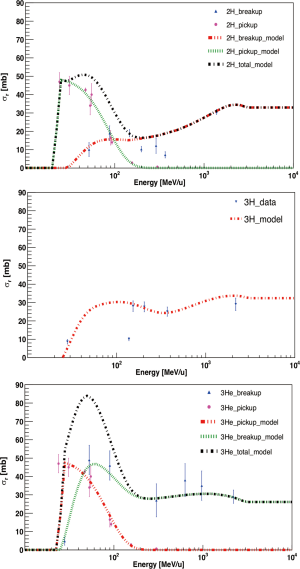
where σr is the total reaction cross section. The cross sections calculated with Eqs. [3-5] are expressed in mb. This formalism was adopted in the new beam model for 4He implemented in TReatment Planning for Particles (TRiP98) (28) and compared to the experimental data (29) as illustrated in Figure 1. Measured breakup and pickup cross sections agree with the model calculation within their error bars (around 15% or less) and can be considered an acceptable result. In fact, it has been demonstrated that a discrepancy up to 20% in the nuclear interactions models implemented in the TPS has an impact on RBE-weighted dose of the order of 1% and on the dose up to 10% at a SOBP (30). This value gets smaller considering smaller target volumes. For 4He, once empirical total fragmentation cross sections were implemented in TRiP98, dosimetry and radiobiological experiments were performed and compared with the code showing a good agreement (29).
All nuclear fragmentation processes described above produce a mixed secondary radiation field that needs to be characterized. Total charge-changing cross sections give information on the primary beam flux attenuation when traveling in matter while partial charge-changing cross sections are related to the fragments build up. Additionally, double differential cross sections of primary and secondary particles are necessary to reproduce their kinetic energy spectra and angular distribution.
These data represent a platform for TPS to predict the correct number of ions that have to be delivered to the tumor as well as to estimate the out-of-field dose. A major complication in evaluating the delivered dose arises from the fact that the LET distribution has to be known in each point of the treatment volume (19,28,31).
Attenuation curves
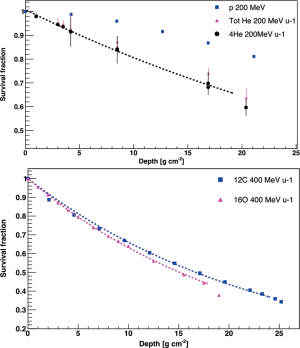
Measurements of the primary beam absorption are essential to gain information on the different interactions processes. By comparing the number of primary particles impinging on the target (N0), with those surviving the target (N), it is possible to get the “survival fraction” of the beam in its whole range. The slope of this survival curve provides an estimate of the mean free path λ, which can be expressed in the form of a Beer-Lambert law N = N0e−x/λ, and it is proportional to the nuclear fragmentation cross section (λ = 1/NMσfc, where NM is the number of atoms or molecules inside the target). This parametrization cannot be applied to protons. As explained in the section above, nuclear interactions of protons with matter lead to the production of secondary protons indistinguishable from the primaries, which causes an increase of the proton yield instead of an attenuation. However, for simplicity and an easier readability of this section the word “attenuation” will be used also for protons. Examples of survival curves for 12C, 16O, 4He and protons are presented in Figure 2.
For 12C and 16O ions, the data are well fit by a single exponential function, meaning that the energy dependence of the total reaction cross section in this energy range is small (32). Often it is difficult to identify the isotopes of these heavy ions without a proper fragment separator system, therefore only the total amount of carbon or oxygen are measured giving information on the charge-changing processes, which in this case are dominant.
Protons do not show an exponential decrease but a build up with depth due to secondary protons produced via nuclear interactions. For this reason, it is essential that TPSs include modeling for target fragmentation processes. For Helium instead, an exponential decrease can be observed once a proper separation between 4He and its neutron-deficient isotope 3He is achieved. Once the contribution of the latter has been subtracted, the λ calculated from the exponential fit of the 4He data points gives the total fragmentation cross section (21).
Cross sections of protons and 12C ions
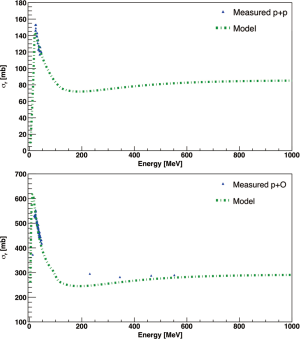
Carlson et al. (33) presented a database where total reaction cross sections of protons interacting with all complex nuclei at beam energies up to 1 GeV are collected. An overview of the available experimental cross sections measured in Hydrogen and Oxygen targets, of interest for therapy applications, is presented in Figure 3 as a function of the protons kinetic energy. Especially for p+1H and p+16O reactions, there is a big gap of experimental data in the therapeutic energy range (between 50 and 230 MeV). For protontherapy applications, it is essential to characterize the cross sections related to the production of target fragments, which might have a high-LET and thus give a significant contribution to the dose deposited in the healthy tissue between the entry channel and the Bragg peak (35). The Italian National Institute of Nuclear Physics (INFN) funded experiment called FragmentatiOn On Target (FOOT) is dedicated to the investigation of target fragmentation of primary proton beams interacting with different targets and will carry on an experimental campaign to fill the gaps of available measured cross sections for this process.
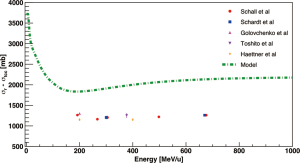
Experiments to investigate Carbon fragmentation relevant for therapy were mainly performed at GSI and HIMAC. Golovchenko et al. (36,37) measured the spatial and momentum distribution of fragments produced in water by 12C beams in the energy range of 110–334 MeV/u. An extensive study of the Carbon interaction with thick water targets has been presented by Haettner et al. (19) and Gunzert-Marx et al. (20), which included double differential cross sections and a characterization of secondary neutrons. Schall et al. (38) studied the total charge-changing cross sections of 12C ions in polymethyl methacrylate (PMMA) and water with energies between 190 and 600 MeV/u. Schardt et al. (32) studied total charge-changing cross sections for 12C ions on water at 670 and 300 MeV/u. Matsufuji et al. (39) investigated fragmentation of a 290 MeV/u 12C beam in water while Toshito et al. (40) measured total and partial charge-changing cross sections of 200 and 400 MeV/u 12C ions in water and polycarbonate.
Total charge-changing cross sections of 12C on elemental targets have been studied by Zeitlin et al. (41), Ferrando et al. (42) and Webber et al. (43) for carbon with energies between 200 and 1,000 MeV/u impinging on graphite, polyethylene, helium, aluminum, copper, lead and tin. The combination of Graphite and Polyethylene data provides an indirect measurement for Hydrogen and could be exploited to estimate target fragmentation cross sections for proton beams applying the cross section combination property (38).
A collection of total charge-changing cross sections for 12C ions interacting with water is plotted in Figure 4 as a function of the beam kinetic energy. Total reaction cross sections calculated with Sihver’s model are always higher than the experimental data because the latter are total charge-changing cross sections and thus only include reaction channels where at least one protons have been removed.
Cross sections of 4He and 16O ions
As shown in Figure 5, the collection of published total reaction cross sections of 4He beam on elemental or tissue equivalent targets revealed a “gap” in the therapeutic energy range. Measurements of 4He on protons, 12C and 16O were performed by Auce et al. (45) and Ingemarsson et al. (46) at low primary beam energy (below 100 MeV/u), while studies published by Webber et al. (43), Ferrando et al. (42) and Jaros et al. (48) presented total charge-changing cross sections at energies above 500 MeV/u.
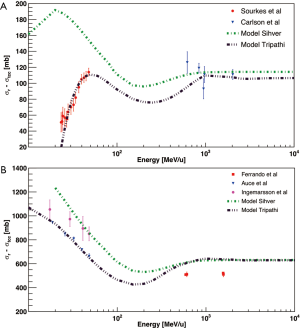
Two recent works of Marafini et al. (22) and Rovituso et al. (21) studied the fragmentation of Helium in tissue equivalent targets. The former measured angular distributions and kinetic energy spectra of secondaries after the Bragg peak for 102, 125 and 145 MeV/u 4He beams impinging on PMMA, from which double differential cross sections could be estimated. The work of Rovituso et al., instead, focused not only on the double differential cross sections of the secondaries but also on the attenuation of the primary beam flux in water and PMMA targets at two energies (120 and 200 MeV/u). From the latter measurement the mean free path λ and the corresponding total fragmentation cross section were estimated. The results obtained in this work are presented in Table 1 together with predictions from three theoretical models (25,34,49). As the calculations have no associated error, a quantitative comparison between experimental and theoretical values is not possible. Based on a qualitative analysis, data reported in Table 1 indicate overall a fair agreement.

Full table
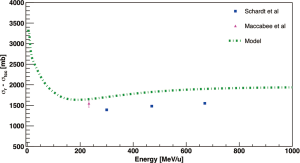
The works of Schall et al. (38), Schardt et al. (32) (complementary works) and MacCabee et al. (50), measured total charge-changing cross sections of 16O beams impinging on H2O targets. The results are presented in Figure 6 together with a total reaction cross sections calculated with the Sihver et al. model (25). As for Figure 4, theoretical values are higher than the experimental data because they include also non-charge-changing reactions channels. Weber et al. (43) measured total and partial charge-changing cross sections of 16O beam on Helium target at 640, 1,600, 591 and 1,563 MeV/u, while Auce et al. (45) and Ingemarsson et al. (46) measured total reaction cross sections of 4He beam on 16O target for energy beam between ~70 and ~190 MeV/u. In order to implement 4He and 16O ions in radiotherapy, additional measurements are required to fill the gap in the therapeutic energy range and provide data to develop and verify the TPS models as well as for benchmarking Monte Carlo transport codes.
Depth dose profile
The depth dose profile of a moderately relativistic charged particle in matter is ruled by the energy loss through electromagnetic Coulomb interactions (excitation or ionization of the atomic shell electrons) and its theory has been described extensively elsewhere (9,31). However, the physical processes described in “Section Nuclear interactions” can act as coadjuvant or antagonist to ionization and thus impact the trend of the curve. The first step for understanding advantages and disadvantages of Helium and Oxygen in CPT is then to compare their Bragg curves to protons and Carbon at similar penetration depths. Experimental dose profiles in High Density Polyethylene (HDPE) are reported in Figures 7,8.
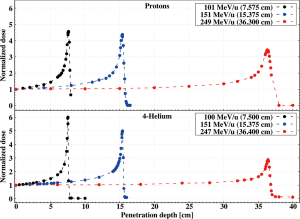
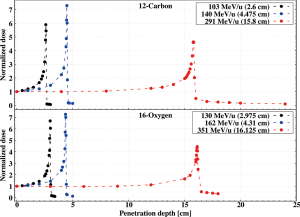
For each pair, the energies have been selected so that the ions have the same range. All curves are normalized to the dose value at the entry channel and have been measured at the NASA Space Radiation Laboratory (51) inside Brookhaven National Laboratory (Upton, NY, US). A more extensive collection of results can be found in the work of Tessonnier et al. (Figure 2) (52).
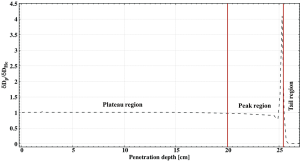
To investigate how the behavior of these curves is influenced by the different interaction processes, three regions have been identified as representative: the plateau in the proximity of the entrance channel, the area around the Bragg peak and the tail.
The slowing down mechanism is mainly dominated by inelastic collisions with the target electrons and its probability increases with decreasing ions velocity. If the ions initial energy is high enough (i.e., for treating deep-seated tumors), this region is rather flat as the LET is quasi-energy independent. On the other hand, for low-energy beams (~100 MeV/u), the rise is almost immediate as a small drop of the beam kinetic energy results in a large increase of the LET and hence of the dose deposited.
As ions penetrate deeper in the medium, both nuclear fragmentation and multiple Coulomb scattering start playing a major role. As illustrated by the ablation-abrasion theory (Section “Nuclear interactions”), beam particles are substituted by lighter fragments of approximately the same energy and thus lower LET. In first approximation, the dose reduction δD in this region is linear with the total fragmentation cross section σtf and target areal density ρx (53):
Furthermore, primary ions deviate from their initial direction due to multiple Coulomb scattering and end up losing their energy outside the beam core. Both Coulomb and nuclear processes cause a decrease of the overall dose deposition along the initial direction which counteracts the increase due to the slow down. On the other hand, secondaries originated from projectile or target fragmentation (Section “Nuclear interactions”) might have a very high LET and thus contribute synergistically with the dose increase due to the primary beam energy loss. The LET dependence on Z2 makes target fragmentation more relevant for proton than for heavy ion beams.
In the proximity of the Bragg peak, elastic collisions with the target nuclei begin to contribute significantly to the slow down and eventually dominate the stopping process in the last few µm of the ions path. The Bragg peak parameters are defined by all interaction mechanisms discussed above. Its height is strongly affected by nuclear fragmentation while its width is dominated by the range straggling. The abrasion-ablation theory states that vf ≈ vp and that most fragments are produced with an energy similar to the primaries. In addition, the Fermi momentum provides a further energy boost which results in the production of light secondaries with an energy up to twice as much the projectile energy. These fragments, together with secondaries produced in the proximity of the peak, have a range longer than the primary radiation and keep depositing energy inside the target once all projectiles have stopped, creating a tail.
On the bases of these considerations, the experimental Bragg curves of Figures 7,8 and from (52) can be discussed. In the analysis, simulated depth dose profiles published in (54) and shown in Figures 9-11 are also exploited.
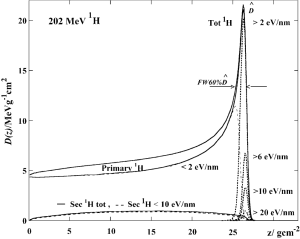
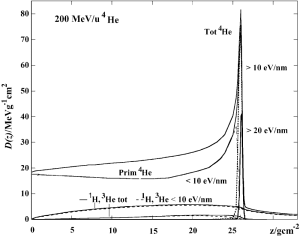
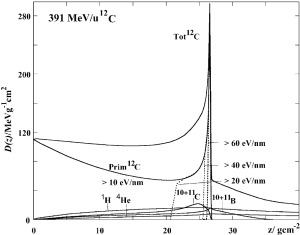
To investigate the differences in the Bragg curves behavior, the ratios δDp/δDHe and δDC/δDO of the energy deposited at a given depth have been calculated from simulations with PHITS Monte Carlo code (55). The initial energies have been chosen so that the compared beams have the same range. For each ion, theδD values are normalized to the entry channel to eliminate the dependence from the LET and highlight the effects of fragmentation, lateral scattering and range straggling. A ratio equal to ~1 means that the Bragg curves of the two ions have the same trend.
Independently of the beam initial energy, the plateau region for Helium and protons appears to have the same trend and its ratio remains constant around 1 till the beginning of the peak region (Figure 12). As protons can only produce target fragments (i.e., particles with equal or higher LET), there is no process that counteracts the slow down. This is well illustrated in Figure 9, where both the overall dose curve and the contribution from the primary protons increases steadily with increasing target depth.
For Helium, nuclear fragmentation acts against the LET change of the beam, resulting in a fall off of the energy loss from the primary ions (curve labelled as “Prim 4He” in Figure 10). However, the Helium overall dose curve (Figure 10), which includes also the contribution from secondaries, and its comparison with protons in Figure 12 indicate that the two ions have the same trend, steadily increasing their energy loss with increasing depth. This result originates from fragmentation. The most abundant secondaries produced by 4He are protons, which also give the highest contribution to the dose compared to all other fragments in the plateau region. Secondary protons produce target fragments and their depth dose curve follow the trend typical of protons shown in Figure 9. The total charge-changing cross section of 4He is twice as high as protons [636 (21) vs. 352 (49) mb for 200 MeV/u beams in water] but is only half than Carbon. Thus, the drop in energy loss of the primary Helium caused by its fragmentation (Figure 10) is compensated by the contribution from secondary protons and results in an overall increase of the dose deposition. The rate at which the dose increases is the same for primary protons and Helium, as the ratio δDp/δDHe is ~1 over the entire plateau.
The behavior of the two ions starts deviating in the peak region at 20 cm depth, where the ratio δDp/δDHe drops from 0.98 to 0.80 within 2 cm. The faster rise of the Helium curve is mainly due to secondary fragments, which mostly have similar (protons) or smaller (3He) range than the primary beam and thus stop upstream of the peak. Fragmentation has also the effect of decreasing the peak height, because less primary ions arrive to the target location. These effects become more and more pronounced at higher initial energies, where more material has to be traversed by the beam to reach its stopping point. However, even at 200 MeV/u, which is almost at the top end of the therapeutic energy range, the Helium peak remains 1.27 times higher than protons (the ratio δDp/δDHe at this depth is equal to 0.79).
Immediately downstream of the 4He Bragg peak, the ratio δDp/δDHe rises very sharply. This behavior is due to the angular straggling, from which protons suffer much more than Helium, and that causes a broadening of their peak. Thus, while all 4He ions have stopped, there is still a large fraction of primary protons left. This region extends several mm deeper than the 4He beam stopping point. This effect gets even more visible at low energies, where the lateral straggling is more pronounced.
Once all protons have ranged out, their dose curve drops to zero while the Helium profile shows a tail caused by the fragments (compare Figures 9,10).
The deviations between Oxygen and Carbon Bragg curves are different than protons versus Helium as they are both heavy ions and have a closer atomic mass number and charge. The ratio δDC/δDO rises steadily from the entrance channel up to a 6% increase at the Bragg peak position. Figure 13 proves that for Carbon the dose deposited by secondary fragments does not compensate for the loss of primary ions, which has a much higher LET. This is even more dramatic for Oxygen, which suffers higher fragmentation as indicated by the data reported in Figure 6 and Eq. [6]. In this case, the worst-case scenario in therapy is given by the highest energy employed, which is the one plotted in Figures 11,13. The curves illustrated in Figure 8 and from Tessonnier et al. (52) show that this effect is attenuated at lower energies, where the primary beam slowing down dominates the profile shape and the dose begins to rise immediately at the entry channel. This behavior is due to the fact that the dose deposition δD strongly depends on the beam energy in the therapeutic range while the total charge-changing cross section σtcc is quasi-constant as shown in Figures 4,6. The ratio δDC/δDO at the peak increases with increasing beam energies, starting at around 0.8 and rising up to 1.06.
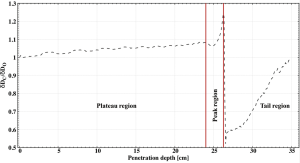
As for the ratio δDp/δDHe, the source of the spike just downstream of the 16O Bragg peak is lateral straggling, which causes the 12C peak to be wider. However, in this case this region spreads less than 2 mm after the peak because the difference in lateral straggling between Oxygen and Carbon is not as severe as between protons and Helium.
The larger fragmentation cross section for 16O ions also results in a higher and longer tail than for Carbon, which extends several centimeters downstream of the Bragg peak.
Lateral profile
Nuclear fragmentation processes do not affect only the depth dose profile but also the lateral beam distribution. To investigate this effect, Gottschalk et al. (26) proposed to divide the lateral profile in two regions: the core, which contains the primary beam contribution, and the halo, i.e., the low dose region produced by the secondary fragments. The single Coulomb scattering described by Rutherford gives really small lateral deviations. In a thin target, if the number of scattering events increases but remains under few tens of interactions the process is referred to as multiple scattering and it is difficult to model. For a thick absorber, instead, the MCS is responsible for the lateral diffusion, which is often parametrized with a Gaussian distribution characterized by a standard deviation σθ given by the Highland approximation (11). However, measurements of an ion beam lateral diffusion in air and/or after some materials indicate that the simple Gaussian approach cannot reproduce the halo region. This effect is extremely important especially for protons and must be addressed properly for a correct dose delivery in a treatment. The lateral scattering in air, in monitor devices placed along the beam line, in the energy modulator and inside the patient’s body has to be correctly parametrized to get a realistic, uniform and precise dose distribution around the tumor volume.
Monte Carlo codes require a substantial amount of computational time to simulate a scattered lateral dose profile distribution, therefore analytical parametrizations are implemented inside the TPS. A common approach used in protontherapy has been proposed by Soukup et al. (56) and describes the lateral dose distribution with a double Gaussian function, one for reproducing the core and one for the halo.
A study on possible parametrizations for protons was performed by Bellinzona et al. (57), where different functions were compared in terms of best χ2, number of free parameters and computational time (Figure 14). The work proved that a function composed by the sum of a Gaussian and a hyperbolic function (called Rutherford function) is the best compromise in terms of free parameters and computational time.
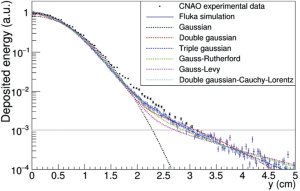
A previous study from Parodi et al. (58) used the double Gaussian approach to describe also a scattered Carbon beam profile and showed that the agreement is not very good with the experimental data in the halo region. Several works from Inaniwa et al. (59-61) show that a triple Gaussian parametrization describes well the Carbon ions profile. In all these works, the simulation given by the Monte Carlo codes was definitely superior in terms of agreement with the experimental data but too consuming in terms of computational time.
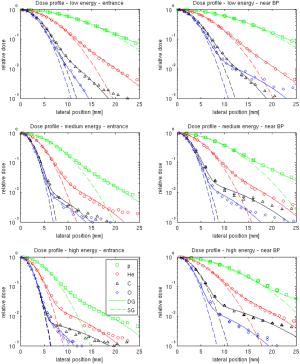
For 4He and 16O beams new experimental data have been published by Tessonnier et al. (52). Different profiles were compared at different depths (entrance, plateau and near the Bragg peak), and they were parametrized with a single Gaussian or a double Gaussian function. The results indicated that the Gaussian component used to reproduce the halo is broader for protons and gets narrower with increasing beam charge (Figure 15).
Discussion
The physical properties of 4He and 16O ions have been presented in this work and compared with protons and 12C particles, respectively. The review focused on nuclear interactions and how they influence the beam depth dose curve and lateral profile.
Nuclear fragmentation changes the beam composition, energy and spatial distribution. In a typical treatment, up to 50% of Carbon ions break up while protons undergo approximately 1% nuclear interactions per cm of water traversed. The charge and LET of secondaries might be lower or higher than the primary radiation and the majority is emitted in the forward direction, although there is an isotropic component. Fragments build up causes a drastic dose reduction from its initial value at the entry channel, effects the Bragg peak characteristics and deliver dose out-of-field. Secondaries ranging out in the proximity of the peak enhance the dose gradient between the plateau and the peak while the loss of primary ions fragmented decreases the peak height. The residual dose deposited in the curve tail also originates from fragments. Among the alternative heavy ions considered here, Helium has the lowest total fragmentation cross section and Oxygen the highest.
Lateral scattering, due to multiple Coulomb interactions of the projectile with the target nuclei, causes the beam (and its fragments) to deviate from the initial trajectory and its probability increases with decreasing A and energy of the ion. This effect becomes extremely important in the proximity of the stopping point, where particles have very little energy left, and leads to a broadening of the lateral profile. Being the lightest particle, protons heavily suffer lateral scattering, not only in the patient but also in any beam line element, monitoring device and air gap.
Electromagnetic interactions with target electrons are responsible for particles slow down. As the projectile energy loss is proportional to its Z2, protons have the lowest LET at the entry channel but also the lowest dose-averaged LET (62) [] at the peak position, as indicated by data reported in Table 2.

Full table
Fluctuations in energy loss are responsible for increasing the Bragg peak width. At a given range, the relative energy straggling compared to protons is 2 times smaller for Helium, 3.5 time smaller for Carbon and 4 times smaller for Oxygen.
The absolute dose profiles per unit fluence plotted in Figure 16 (3) summarizes all physical properties mentioned above.
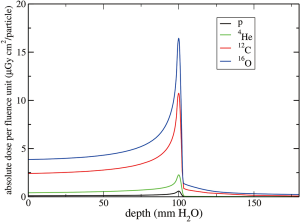
To understand the rational of using other ions in radiotherapy, the physical advantages have to be combined with biology and clinical benefits. One of the fundamental principles is to deliver a dose as high as possible to the target volume and as low as possible to the healthy tissue to avoid side effects. The LET is usually identified as a key parameter to link the physical properties of the radiation with its biological effects. Figure 16 shows that for beams with 10 cm range in water Oxygen has the highest LET at the peak but also at the entrance channel. Furthermore, a heavier beam undergoes less lateral and range scattering but its fragmentation tail is more pronounced. Light ions deposit less dose along their path to the tumor, their tail is small (Helium) or negligible (protons) but they suffer more spatial spreading and their LET at the peak might not be high enough to kill radioresistant tumors, as those in hypoxic conditions.
All these features are enhanced or become negligible in the calculation of a treatment plan, where several energies are combined to produce a Spread Out Bragg Peak (SOBP) and the physical dosimetry is optimized on the bases of biology data. An example is shown in Figure 17 (64), where treatment plans for a chordoma of the skull base calculated with the latest version of TRiP98 (28,29) are shown for protons, Helium or Carbon ions.
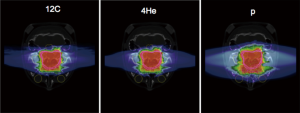
The figure illustrates that only Carbon and Helium beams spare the organs at risk (OAR) marked in yellow, because their dose gradient at the margins is very sharp. Instead, protons undergo enough lateral straggling to smear the beam and irradiate also the OAR. Oxygen would perform even better than Carbon and, having a higher dose-averaged LET, would also cause a significant reduction of the OER. On the other hand, the use of 12C ions on pediatric patients is very controversial because of the concern for the risk of inducing secondary cancers caused by the high-LET in the plateau and Oxygen would be even worse. Furthermore, the unavoidable fragmentation tail forbids the application to those patients where the OAR are located in a position which requires the treatment to be delivered with a single field. An example is the craniospinal irradiation for medulloblastoma illustrated in (2).
Helium represents a very attractive alternative to current ions used in radiotherapy. It has a much smaller lateral straggling than protons and close enough to Carbon to produce a dose profile with sharp margins, as shown in Figure 17. Helium undergoes significantly less fragmentation than all other heavy ions and thus has a limited dose tail behind the SOBP. Furthermore, it is the only ion species that produces most of its secondaries with equal or smaller range. Helium LET at the entrance channel is low and thus would not represent a concern for pediatric cases as much as 12C. The LETD(E) increase at the peak makes it more effective than protons in the treatment of radioresistant tumors.
Conclusions
The physical processes illustrated in this review pointed to the advantages and disadvantages of the current and potential ions used in radiotherapy. When these data are combined with radiobiology, it becomes clear that the idea of a “magic bullet” optimal for all patients is impossible. The most advantageous approach should select the ion type on a case-by-case base. From this point of view, enlarging the pool of candidate radiation would be very beneficial. The data collected in this investigation indicate that Helium represents an extremely valid alternative to protons and Carbon, especially for pediatric patients. Unlike Helium, Oxygen will be mainly used as a boost in combination to protons or Carbon to treat radioresistant regions of the tumor which require a high LET to be killed.
One of the first steps to accomplish this goal is to have TPSs optimized for the new ions, either extending the existing versions or developing new ones. Experimental data available in literature to characterize the physical processes of interest discussed here showed a “gap” in the therapeutic energy region and call for additional measurements. On the other hand, existing theoretical approaches can be already adapted to model Helium and Oxygen interactions with matter and thus to reproduce acceptable depth dose and lateral profiles.
Acknowledgments
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Marco Durante, Giusi I. Forte, Giorgio Russo) for the series “Radiobiological models towards a personalized radiation oncology” published in Translational Cancer Research. The article has undergone external peer review.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tcr.2017.06.46). The series “Radiobiological models towards a personalized radiation oncology” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- PTCOG. Particle therapy facilities in operation (2017). Available online: https://www.ptcog.ch/index.php/facilities-in-operation
- Newhauser WD, Durante M. Assessing the risk of second malignancies after modern radiotherapy. Nat Rev Cancer 2011;11:438-48. [Crossref] [PubMed]
- Tommasino F, Scifoni E, Durante M. New ions for therapy. Int J Particle Ther 2015;2:428-38. [Crossref]
- Tinganelli W, Durante M, Hirayama R, et al. Kill-painting of hypoxic tumours in charged particle therapy. Sci Rep 2015;5:17016. [Crossref] [PubMed]
- Scifoni E, Tinganelli W, Weyrather WK, et al. Including oxygen enhancement ratio in ion beam treatment planning: model implementation and experimental verification. Phys Med Biol 2013;58:3871-95. [Crossref] [PubMed]
- Bassler N, Jäkel O, Søndergaard CS, et al. Dose- and LET-painting with particle therapy. Acta Oncol 2010;49:1170-6. [Crossref] [PubMed]
- Sokol O, Scifoni E, Tinganelli W, et al. Oxygen beams for therapy: advanced biological treatment planning and experimental verification. Phys Med Biol 2017; [Epub ahead of print].
- Bethe HA. Molière’s theory of multiple scattering. Phys Rev 1953;89:1256-66. [Crossref]
- Durante M, Paganetti H. Nuclear physics in particle therapy: a review. Rep Prog Phys 2016;79:096702 [Crossref] [PubMed]
- Bednyakov AA. On the Molière theory of multiple scattering of charged particles (1947–1948) and its critique in subsequent years. Physics of Particles and Nuclei 2014;45:991-9. [Crossref]
- Highland LV. Some practical remarks on multiple scattering. Nucl Instrum Methods 1975;129:497-9. [Crossref]
- Serber R. Nuclear reactions at high energies. Phys Rev 1947;72:1114. [Crossref]
- Glauber RJ. Boulder summer school lecture notes. In: Brittin WE, Dunham LG. editors. Lectures in theoretical physics. New York: Interscience Publishers Ltd., 1959.
- Hüfner J, Schäfer K, Schürmann B. Abrasion-ablation in reactions between relativistic heavy ions. Phys Rev C 1975;12:1888-98. [Crossref]
- Gaimard JJ, Schmidt KH. A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reaction. Nucl Phys A 1991;531:709-45. [Crossref]
- Campi X, Hüfner J. Nuclear spallation-fragmentation reactions induced by the high-energy projectiles. Phys Rev C 1981;24:2199-209. [Crossref]
- Goldhaber AS. Statistical models of fragmentation processes. Phys Lett B 1974;53:306-8. [Crossref]
- Zeitlin C, La Tessa C. The role of nuclear fragmentation in particle therapy and space radiation protection. Front Oncol 2016;6:65. [Crossref] [PubMed]
- Haettner E, Iwase H, Krämer M, et al. Experimental study of nuclear fragmentation of 200 and 400 MeV/u (12)C ions in water for applications in particle therapy. Phys Med Biol 2013;58:8265-79. [Crossref] [PubMed]
- Gunzert-Marx K, Iwase H, Schardt D, et al. Secondary beam fragments produced by 200 MeV u−1 12C ions in water and their dose contributions in carbon ion radiotherapy. New J Phys 2008;10:075003 [Crossref]
- Rovituso M, Schuy C, Weber U, et al. Fragmentation of 120 and 200 MeV u-14He ions in water and PMMA targets. Phys Med Biol 2017;62:1310-26. [Crossref] [PubMed]
- Marafini M, Paramatti R, Pinci D, et al. Secondary radiation measurements for particle therapy applications: nuclear fragmentation produced by 4He ion beams in a PMMA target. Phys Med Biol 2017;62:1291-1309. [Crossref] [PubMed]
- Povh B, Rith K, Scholz C et al. Particle and Nuclei. Berlin: Springer, 2008.
- Bradt HL, Peters B. The heavy nuclei of the primary cosmic radiation. Phys Rev 1950;77:54-70. [Crossref]
- Sihver L, Mancusi D. Present status and validation of HIBRAC. Radiat Meas 2009;44:38-46. [Crossref]
- Gottschalk B, Cascio EW, Daartz J, et al. On the nuclear halo of a proton pencil beam stopping in water. Phys Med Biol 2015;60:5627-54. [Crossref] [PubMed]
- Cucinotta FA, Towsend LW, Wilson JW. Description of alpha-nucleus interaction cross sections for cosmic ray shielding studies. NASA Technical Paper 1993;3285:1-42.
- Krämer M, Durante M. Ion beam transport calculations in treatment plans in particle therapy. Eur Phys J D 2010;60:195-202. [Crossref]
- Krämer M, Scifoni E, Schuy C, et al. Helium ions for radiotherapy? Physical and biological verifications of a novel treatment modality. Med Phys 2016;43:1995. [Crossref] [PubMed]
- Lühr A, Hansen DC, Teiwes R, et al. The impact of modeling nuclear fragmentation on delivered dose and radiobiology in ion therapy. Phys Med Biol 2012;57:5169-85. [Crossref] [PubMed]
- Schardt D, Elsässer T, Schulz-Ertner D. Heavy-ion tumor therapy: physical and radiobiological benefits. Rev Mod Phys 2010;82:383-425. [Crossref]
- Schardt D, Schall I, Geissel H, et al. Nuclear fragmentation of high-energy heavy-ion beams in water. Adv Space Res 1996;17:87-94. [Crossref] [PubMed]
- Carlson RF. Proton-nucleus total reaction cross sections and total cross sections up to 1 GeV. Atomic Data and Nuclear Data Tables 1996;63:93-116. [Crossref]
- Tripathi RK, Cucinotta FA, Wilson JW. Accurate universal parameterization of absorption cross sections III--light systems. Nucl Instrum Methods Phys Res B 1999;155:349-56. [Crossref] [PubMed]
- Tommasino F, Durante M. Proton radiobiology. Cancers (Basel) 2015;7:353-81. [Crossref] [PubMed]
- Golovchenko AN, Skvar J, Ili R, et al. Fragmentation of 200 and 244 MeV/u Carbon Beams in Thick Tissue-Like Absorbers. Nucl Instrum Methods Phys Res B 1999;159:233. [Crossref] [PubMed]
- Golovchenko AN, Skvarč J, Yasuda N, et al. Total charge-changing and partial cross-section measurements in the reactions of ~110– 250 MeV/nucleon 12C in carbon, paraffin, and water. Phys Rev C 2002;66:014609 [Crossref]
- Schall I, Schardt D, Geissel H, et al. Charge-changing nuclear reactions of relativistic light-ion beams (5 ≤ z ≤ 10) passing through thick absorbers. Nucl Instrum Methods Phys Res B 1996;117:221-34. [Crossref]
- Matsufuji N, Komori M, Sasaki H, et al. Spatial fragment distribution from a therapeutic pencil-like carbon beam in water. Phys Med Biol 2005;50:3393-403. [Crossref] [PubMed]
- Toshito T, Kodama K, Sihver L, et al. Measurements of total and partial charge-changing cross sections for 200-400 MeV/nucleon 12C in water and polycarbonate. Phys Rev C 2007;75:054606 [Crossref]
- Zeitlin C, Guetersloh S, Heilbronn L, et al. Fragmentation cross sections of 290 and 400 mev/nucleon 12C beams on elemental targets. Phys Rev C 2007;76:014911 [Crossref]
- Ferrando P, Webber WR, Goret P, et al. Measurement of 12C, 16O, and 56Fe charge changing cross sections in helium at high energy, comparison with cross sections in hydrogen, and application to cosmic-ray propagation. Phys Rev C Nucl Phys 1988;37:1490-501. [Crossref] [PubMed]
- Webber WR, Kish JC, Schrier DA. Total charge and mass changing cross sections of relativistic nuclei in hydrogen, helium, and carbon targets. Phys Rev C Nucl Phys 1990;41:520-32. [Crossref] [PubMed]
- Sourkes AM, Houdayer A, van Oers WT, et al. Total reaction cross section for protons on 3He and 4He between 18 and 48 MeV. Phys Rev C 1976;13:451-60. [Crossref]
- Auce A, Carlson RF, Cox AJ, et al. Reaction cross sections for 75-190 MeV alpha particles on targets from 12C to 208Pb. Phys Rev C Nucl Phys 1994;50:871-9. [Crossref] [PubMed]
- Ingemarsson A, Nyberg J, Renberg PU, et al. New results for reaction cross sections of intermediate energy α -particles on targets from 9 Be to 208 Pb. Nucl Phys A 2000;676:3-31. [Crossref]
- Rovituso M. Fragmentation and lateral scattering of 120 and 200 MeV/u 4He ions in water targets. Darmstadt: Technischen Universität, 2016.
- Jaros J, Wagner A, Anderson L, et al. Nucleus-nucleus total cross sections for light nuclei at 1.55 and 2.89 GeV/c per nucleon. Phys Rev C 1978;18:2273-92. [Crossref]
- Kox S, Gamp A, Perrin C, et al. Trends of total reaction cross sections for heavy ion collisions in the intermediate energy range. Phys Rev C Nucl Phys 1987;35:1678-91. [Crossref] [PubMed]
- MacCabee HD, Ritter MA. Fragmentation of high-energy oxygen-ion beams in water. Radiat Res 1974;60:409-21. [Crossref]
- La Tessa C, Sivertz M, Chiang IH, et al. Overview of the NASA space radiation laboratory. Life Sci Space Res (Amst) 2016;11:18-23. [Crossref] [PubMed]
- Tessonnier T, Mairani A, Brons S, et al. Experimental dosimetric comparison of 1H, 4He, 12C and 16O scanned ion beams. Phys Med Biol 2017;62:3958-82. [Crossref] [PubMed]
- Durante M. Space radiation protection: Destination Mars. Life Sci Space Res (Amst) 2014;1:2-9. [Crossref] [PubMed]
- Kempe J, Gudowska I, Brahme A. Depth absorbed dose and let distributions of therapeutic H1, He4, Li7 and C12 beams. Med Phys 2007;34:183-92. [Crossref] [PubMed]
- Sato T, Niita K, Matsuda N, et al. Particle and heavy ion transport code system PHITS, version 2.52. J Nucl Sci Technol 2013;50:913-23. [Crossref]
- Soukup M, Fippel M, Alber M. A pencil beam algorithm for intensity modulated proton therapy derived from Monte Carlo simulations. Phys Med Biol 2005;50:5089-104. [Crossref] [PubMed]
- Bellinzona VE, Ciocca M, Embriaco A, et al. On the parametrization of lateral dose profiles in proton radiation therapy. Phys Med 2015;31:484-92. [Crossref] [PubMed]
- Parodi K, Mairani A, Sommerer F. Monte Carlo-based parametrization of the lateral dose spread for clinical treatment planning of scanned proton and carbon ion beams. J Radiat Res 2013;54:i91-6. [Crossref] [PubMed]
- Inaniwa T, Kanematsu N, Hara Y, et al. Implementation of a triple Gaussian beam model with subdivision and redefinition against density heterogeneities in treatment planning for scanned carbon-ion radiotherapy. Phys Med Biol 2014;59:5361-86. [Crossref] [PubMed]
- Inaniwa T, Kanematsu N, Hara Y, et al. Nuclear-interaction correction of integrated depth dose in carbon-ion radiotherapy treatment planning. Phys Med Biol 2015;60:421-35. [Crossref] [PubMed]
- Inaniwa T, Kanematsu N. A trichrome beam model for biological dose calculation in scanned carbon-ion radiotherapy treatment planning. Phys Med Biol 2015;60:437-51. [Crossref] [PubMed]
- ICRU, Linear energy transfer, Technical Report 16. Washington DC, 1970. Available online: http://www.icru.org/home/reports/linear-energy-transfer-report-16
- Tarasov OB, Bazin D. Lise++: Radioactive beam production with inflight separators. Nucl Instrum Methods Phys Res B 2008;266:4657-64. [Crossref]
- Grün R, Friedrich T, Krämer M, et al. Assessment of potential advantages of relevant ions for particle therapy: a model based study. Med Phys 2015;42:1037-47. [Crossref] [PubMed]