
Biomarker adaptive designs in clinical trials
Introduction
Biomarkers are measurable biological indicators of the status of an organism in a particular health condition or disease state. Biomarkers have been discovered and developed to provide information in determining disease diagnosis and prognosis, predicting response to therapies and drug-induced toxicities, and helping in new drug development. Biomarkers have also been utilized in personalized medication to optimize treatment efficacy and safety in clinical practice. In recent years, many cancer treatments benefit only a fraction of the patients to whom they are administered. A high proportion of patients are subject to post-surgery adjuvant chemotherapy; however, approximately 70% of lung cancer patients in stage I are cured by surgery alone (1-3). Recently, development of new cancer drugs have shifted toward molecularly targeted pathways (4-6); it is expected that only a subgroup of patients is likely to benefit from a targeted drug. A goal of cancer trials has become development of a biomarker-based classifier to identify subgroups of patients for whom a new targeted treatment is beneficial. The term ‘biomarker’ has been defined and used in numerous ways for different data types, purposes, and applications (7,8). In drug development, biomarkers can be classified into four categories: prognostic biomarkers, predictive biomarkers, pharmacodynamic biomarkers, and surrogate endpoints (7-11). Prognostic biomarkers predict patients with differing risks of an overall outcome of disease, regardless of treatment. Predictive biomarkers predict the likelihood of patient’s response to a particular treatment. Both prognostic and predictive biomarkers are baseline pretreatment measurements. Prognostic markers classify patients into high-risk and low-risk groups with respect to no-treatment or a standard-treatment. Predictive markers separate patients for whom a particular treatment is effective from patients for whom the treatment is not needed.
Pharmacodynamic biomarkers indicate drug effect on the target in an organism. A pharmacodynamics biomarker provides a link between drug regimen and target effect from the treatment, such as levels of gene expression or microRNA, which is altered by the treatment (12). Pharmacodynamic biomarkers are often used in earlier phases of drug development to demonstrate drug activity, provide information on likely clinical benefit and go/no-go decisions. Pharmacodynamic biomarkers play critical role throughout drug development, from selection of lead compounds in preclinical models to first-in-human trials. A surrogate endpoint is a measure of the effect of a treatment that correlates well with a clinical endpoint (9,10). A surrogate endpoint is used as a biomarker intended to substitute for a clinical endpoint with a faster and more sensitive evaluation of treatment effect (9). Statistical methods for investigation and validation of surrogacy of a biomarker have been reviewed (13-15). Both pharmacodynamic biomarkers and surrogate endpoints measure biological changes from the treatment as indicators of drug activity or treatment efficacy. These biomarkers can be identified only after treatment has been administered to the patients.
Predictive biomarkers are used to develop (binary) classifiers to identify patients as either good or poor candidates for a specific treatment to optimize treatment selection. Development of a predictive-biomarker-classifier consists of two stages: (I) development of the binary classifier and (II) clinical validation of the classifier. Classifier development involves assay development, biomarker identification, and classification algorithm and performance assessment. Clinical validation involves conducting prospectively randomized clinical trials to demonstrate treatment efficacy in the classifier identified patient subpopulation. The patient subpopulation may be included in a whole study patient population (both biomarker positive and biomarker negative patients), or include only biomarker positive patients. Many types of clinical trial designs incorporating predictive biomarkers have been proposed and discussed. These include standard randomized all-patients design, biomarker by treatment interaction design (biomarker-stratified design), biomarker-strategy design, enrichment design (targeted design), and hybrid design (16-19). Figure 1 plots four commonly known designs for biomarker studies. Figure 1A illustrates randomized all patient design in which all patients are randomized first and then test afterwards to determine their biomarker status. Figure 1B illustrates biomarker by treatment interaction design in which patients are tested first and divided into biomarker-defined subgroups. Patients within each biomarker subgroup are randomly assigned to different treatments. Figure 1C illustrates enrichment design, the study patients are selected based on a pre-specified biomarker status and randomly assigned to different treatments. Figure 1D illustrates biomarker-strategy design with a standard control; all patients are randomized to either biomarker-based strategy arm or non-biomarker-based strategy arm. In the biomarker-based arm, the biomarker positive patients receive the treatment and biomarker negative patients receive the standard treatment. All patients in the non-biomarker-based arm receive the standard treatment. Clinical designs for validation of predictive or prognostic biomarkers have been given in detail by Sargent et al. (16) and Buyse et al. (10) and will not be considered in this review.
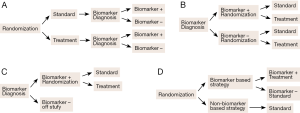
The clinical designs mentioned above have been developed based on the premise that the biomarker or set of biomarkers is available for clinical validation before the start of phase III trial. The study is expected to evaluate a treatment effect in the biomarker defined population. Furthermore, these candidate biomarkers would have been well studied in the phase II developmental stage, the performance characteristics of the classifier are well established in one or more validation studies, and the assay and predictive performance are reproducible and robust experimentally and analytically. However, completely phase II validated biomarkers for uses in the phase III trial are often unavailable (20-22). Clinical trials for targeted drugs can be developed under the framework of drug-diagnostic co-development, which prospectively co-develop a diagnostic test for patient identification in conjunction with a trial for therapeutic efficacy (22-24).
This review is concerned with statistical aspects of biomarker adaptive design for the development of predictive biomarker classifier. The presentation is in terms of microarray gene expression experiments, such as gene expression variables and clinical covariate variables, referred to as genomic variables.
Development of biomarker adaptive designs
Development of predictive classifiers generally consists of three components: biomarker identification, classifier development, and performance assessment (25). These three components represent three major steps involved in the development of prediction models for application to diagnostic, prognostic, and prediction of response. Recently, Freidlin and Simon (20) proposed the adaptive signature design (ASD), which involved biomarker identification and classifier development to the selection of candidate patients and combined with a statistical test for treatment effect in the selected patients. In this section, the ASD is presented as an integrated part of the development of biomarker adaptive clinical trial design.
Biomarker identification
Consider a two-arm experiment with m genomic variables. For a given patient, let xi denote the measurement for the i-th genomic variable (i =1, …, m), t denote the arm indicator (t =0 for control and t =1 for treatment), and yit denote the binary clinical outcome (yit =1 for positive outcome and yit =0 otherwise). Let pit denote the probability of positive outcome from the i-th variable and arm t. Freidlin and Simon (20) proposed an approach to identifying predictive biomarkers by fitting a (reduced) the logistic regression model without the main effect term xi,
This model can be generalized in terms of a generalized linear model (26), by replacing logit link function with the Cox proportional hazards function for survival time data (27), or linear regression function for continuous response data.
The coefficient b2i is the treatment effect regardless of the value of xi, and the interaction b3i is differential treatment effects between the biomarker-positive patients and biomarker-negative patients; that is, treatment effect depends on the value of the predictive biomarkers, xi. These are the markers that predict differential treatment effects. A set of candidate predictive biomarkers can be obtained by identifying those variables xi’s with a significant interaction b3i. The set of significant interaction variables b3i, denoted as U, is used to develop the binary classifier.
Classifier development
A classifier is a mathematical function that translates the set of biomarker values to a set of categories. Two categories are considered; these two categories correspond to predictive outcomes, either positive or negative. Let n denote the total number of patients, and D = (s1, s2, …, sn) be the sampled dataset consisting of n labeled observations. Each sample k (k = 1, 2, …, n) consists of two parts, sk = (xk, yk), where xk is a vector for the set of biomarkers in U, and yk is the class label (1 for positive and 0 for negative) for the k-th observed outcome. The objective is to build a classification rule from the observed dataset D to accurately predict outcome of new sample with the biomarker set x*: p(x* | D) = y* (0 or 1). Given the set of (candidate) predictive biomarkers U, development of a classifier involves two components: (I) selecting a classification algorithm; and (II) specifying the training parameters for the selected algorithm (25).
For binary outcomes such as positive and negative, numerous classification algorithms have been proposed and evaluated for various applications. There include nearest neighbor classification, logistic regression, several variants of linear discriminant analysis, partial least squares analysis, neural network algorithms, naïve Bayes algorithms, shrunken centroids, several variants of classification trees, regression trees, and support vector machines (SVM) (28,29). Recently, Baek et al. (25) found that random forests (RF) (30), SVM (31,32), and diagonal linear discriminant analysis (DLDA) (33) performed well when the number of predictors is large. These three classification algorithms are commonly used in classification and prediction.
Once the classification algorithm is determined, the prediction model needs to be specified before model fitting. Model specification means specifying all aspects of the model parameters, such as specific functional form of the prediction model and tuning parameters. For example, SVM can use either the linear kernel or radial basis function; in the k-nearest neighbor classification, k can be pre-specified or estimated while performing model validation. The ASD approach requires specifying two tuning parameters in classification of patients into subgroups (details are described below).
For quantitative outcomes such as time-to-event outcomes, e.g., survival or disease-free survival, development of a binary classifier is more complex. A common approach is to convert the set of marker measurements into a univariate predictive score, l(x) = ∑ wj xj, where xj’s are biomarker values and wj’s are weights assigned for the j-th biomarker. The weights can be determined by fitting a multiple regression model or by a dimensional reduction approach (34). Specifically, if the number of variables xj’s in U is not large, a multiple logistic regression (or Cox proportional hazards) model is fit using all variables xj’s as predictors. The regression coefficients βj’s of the fitted model are the weights of the biomarker variables xj’s, that is l(x) = ∑ βj xj. Alternatively, the weights can be estimated using the first principal component of the variables xj’s (35). The quantitative predictive scores need to be converted to a binary variable by assigning a threshold cutoff value to divide patients into biomarker-positive and biomarker-negative subgroups. The threshold cutoff is commonly specified at a percentile of the predictive scores or predictive outcomes, such as the median of predictive scores or median of survival time for convenience.
The predictive classifiers described above are to be used in phase III clinical trial designs for biomarker-guided drug development, such as enrichment designs or biomarker-strategy designs. However, it may be difficult to fully establish a biomarker signature before the start of phase III trials (20-22). In some cases, if the candidate biomarkers are known, but, the classifier to define biomarker-positive patients has not yet been fully established or if candidate biomarkers are not known at trial initiation, then biomarker-adaptive designs may be applied (21). The adaptive design combines a test for overall treatment effect in all randomly assigned patients and a classifier to identify biomarker-positive patients with a test for treatment effect in the biomarker-positive patients. In a particular case with one single biomarker, Jiang et al. (36) presented an “adaptive threshold design” to estimate an optimal cutoff by maximization over a number of possible cutoff values. Freidlin and Simon (20) proposed an “adaptive signature design” for a set of potential biomarkers described below.
Adaptive signature designs (ASD)
Biomarker adaptive designs identify most suitable target subpopulations with respect to a particular treatment, based on either clinical observations or known biomarkers, and evaluate the effectiveness of the treatment on that subpopulation in a statistically valid manner.
The ASD consisted of two stages. The data were initially divided into a training set and a test set. The first stage used the training set to identify a set of candidate predictive biomarkers using Eq. [1]. For each gene, the logit model was fit to the training data; the genes with a significant interaction coefficient b3i were selected as predictive biomarkers based on a pre-specified type I error cutoff threshold. The second stage used the training set to identify biomarker-positive and biomarker-negative patients. The ASD used a machine learning voting (MLV) method to identify a biomarker positive subgroup. The procedure requires two pre-specified tuning parameters R and G; the patients are classified as biomarker positive if the predicted treatment versus control odds ratio exceeds a specified threshold R for at least G of the significant genes, that is, exp{b2i + b3i xi} > R or b2i + b3i xi > ln(R), xi ϵ U.
The ASD analysis of the trial consisted of two tests with proper allocation of the significance level of each test to keep the overall type I error controlled at an acceptable level. The first test is a comparison between the treatment and control arms in the whole trial population, the second test is a comparison in the biomarker subgroup population. The ASD design identifies and validates predictive biomarkers with two tests for treatment effect in a single prospective trial. Here, the validation in the subgroup is to test if the predictive classifier is useful for treatment selection.
Performance assessment
Two aims need to be considered in the evaluation of biomarker adaptive design: (I) whether the classifier can classify biomarker-positive and biomarker-negative patients accurately; and (II) whether the treatment is beneficial to the biomarker-positive patient subgroup. Regarding the first aim, the classifier can be evaluated in terms of sensitivity, specificity, and accuracy, as well as positive predictive value (PPV) and negative predictive value (NPV). PPV is the probability that a selected biomarker-positive patient is truly biomarker-positive and NPP is the probability that a selected biomarker-negative patient is truly biomarker-negative. PPV and NPP are more relevant measures of predictive performance; these two quantities directly measure the proportions of correct identifications for these two subgroups. Additionally, receiver-operating characteristic (ROC) curves are a statistical graphic method widely used to provide a summary measure for evaluation of medical diagnosis. A ROC curve is a plot of sensitivity as function of (1-specificity) for different cut-off points of a decision threshold. The area under the ROC curve, called the AUC or c-statistic, is a measure of how well a model discriminates patients into two classes. Regarding the second aim, primary evaluation is the power to detect a treatment effect in the biomarker-positive group. The power depends on the performance of the first aim, sample size, and type I error allocation between the overall test and subgroup test. For a given sample size and significance level, a classifier with higher sensitivity and specificity should be more powerful to detect treatment effect.
The most important consideration in the evaluation of a procedure is to unbiasedly assess its “performance”, which includes the classifier’s accuracy and power to detect treatment effect. To obtain unbiased estimates, the current sampled data are divided into a training set and a separate test set. The training set is used for model development, and the test set is used for performance assessment. The key principle is that the test data should never be used in the model development, including biomarker identification, classifier development, and testing for treatment effect in subgroup analysis.
The split-sample and cross-validation methods are commonly used to assess performance of a classifier. The split-sample method randomly splits the data into two subsets (either the entire data or a designated test dataset), a training set for model building and a test set for model validation. Split-sample validation is known to have large variance, especially when the sample size is small. The precision may be improved using resampling techniques. Specifically, cross validation involves repeatedly splitting the sampled data into a training set and test set to generate different training and test sample partitions to repeatedly estimate “accuracy”. The averaged “accuracy” from different training-test partitions is the classifier “accuracy” (25). The split-sample method provides a single performance analysis. The cross-validation can be regarded as a multiple split-sample validation. The cross-validation provides more stable estimates and the uses of the data efficiently. The original ASD (20) used a split sample validation for performance assessment. A more powerful version, “cross-validated adaptive signature design” (37), was proposed recently. The cross-validation method was applied to tune the parameters to improve performance of the classifier (37,38).
Statistical issues in the development of biomarker adaptive designs
Interaction test
The traditional statistical approach to determining if the i-th variable xi is associated with a treatment response yit is to fit the full generalized linear regression model, including xi and treatment t as main effects and the interaction (xi*t):
The difference between Eqs. [1] and [2] is that Eq. [2] includes the main effect b1i xi for an association between the i-th gene xi and the response yi0. In the standard statistical modeling, the initial model typically starts with main effects and adds interaction terms as appropriate. Therefore, it would not test interactions without the main effects present in the model. However, it is well known that the power for assessing interaction effects using Eq. [2] is often poor; a primary reason is that the sample size is calculated to address the main effects. Eq. [1] should have more power to detect an interaction effect than Eq. [2], and, therefore, is useful for identification of predictive biomarkers.
If the interaction b3i is significant, then the predictive variable xi may be regarded as a (candidate) predictive biomarker. It should be noted that a significant interaction does not automatically imply that the variable is predictive. When the interaction effect is significant, the hazard ratio (HR) is a useful statistic for quantifying the treatment effect and the interaction effect. The HR of the treatment to the control with respect to xi is HR(xi) = exp(b2i + b3i xi).
Subgroup analysis
Subgroup analysis is referred to as an evaluation of treatment effects in specific subgroups of patients defined by baseline characteristics. Subgroup analysis has a long history of addressing the heterogeneity of treatment effects across patient subgroups of interest (39-45). In general, there are two possible situations that may involve subgroup analysis: (I) an overall treatment effect and a differential subgroup effect; and (II) no overall treatment effect but a differential subgroup effect. In the first situation, subgroup analysis is conducted to demonstrate that there is consistency in the effect across various subgroups, and/or that certain subgroups may experience greater benefits or harms than others. In the second situation, subgroup analysis is conducted to show that there is a ‘statistically significant’ treatment effect in one or more subgroups. The second situation commonly occurs when the overall treatment effect has marginal significance (or no significance). One major criticism is that the subgroups are determined in the post hoc analysis. These types of subgroup analyses are considered as descriptive and exploratory, and do not provide validation evidence for subgroup treatment effects. When the interaction effect is significant, there may be four possible comparisons of interest: comparisons of control versus treatment arms for the biomarker positive and biomarker negative patients, and comparisons between biomarker positive versus biomarker negative patients within the control arm and within the treatment arm. In confirmatory clinical trials, the subgroup should be defined by baseline characteristics and analysis should be pre-specified with proper control of the type I error rate. More comprehensive discussion of subgroup analysis in tailing clinical trials is published in the reports (44,45).
An interaction test between the treatment and subgroup is a commonly used statistical method for assessing the heterogeneity of treatment effects among subgroups of a baseline (predictive) variable. This approach performs one statistical test irrespective of the number of subgroups. Each variable defines a characteristic of a subgroup. The set of predictive biomarkers jointly defines the biomarker positive and negative subgroups. In order to identify all potential predictive biomarkers, the interaction test must be performed for each genomic variable among all variables considered in the study. Since many tests are performed, the level of significance needs to be adjusted to account for false positive findings.
Multiple testing
Subgroup analysis typically involves a test of hypothesis of treatment effect in all patients and a test in biomarker-positive subgroup; it may test or estimate the treatment effect in the biomarker-negative subgroup depending on the study objectives. A P value is computed in each test. When the P value is less than or equal to the predetermined level of significance α. the test concludes that there is a significant treatment effect with the type I error rate of no more than α. The level of significance is defined under a single test. If more than one test is conducted, the level of significance of individual tests needs to be adjusted so that the overall type I error rate is no more than α. The Bonferroni adjustment is the simplest method to account for the multiple testing problem; the Bonferroni adjustment divides the significance level of each test by the number of tests performed. If two tests are performed, Bonferroni uses 2.5% significance level for each test to ensure an overall 5% error rate. In subgroup analysis, the overall 5% type I error can be allocated among the test to be performed. For example, the procedure can be performed at 4% significance level for the overall effect and 1% for the subgroup effect.
The hierarchical (fixed sequence) testing procedure is a useful approach to applying to subgroup analysis (46) without adjustment of the level of significance. The testing procedure is hierarchically structured starting with the test of the primary hypothesis. If the null hypothesis is not rejected, the procedure stops; only the rejection of the hypothesis permits testing the next hypothesis. When the treatment effect on the biomarker-positive patients is the primary interest, the testing procedure can be structured as follows. Suppose the test for treatment difference between treatment and control in all patients is set at 2% significance level. The subgroup analysis can start with the test in the biomarker-positive patients using 3% significance level if the test in all patient hypotheses is significant. If the test in the biomarker positive patients is not significant, then the procedure stops. Otherwise, it is possible to compare the treatment to the control in the biomarker-negative patients using 3% significance level if formal testing of this hypothesis is part of the study objectives. This sequential approach controls the overall false positive rate at 0.05.
When the number of tests is large, such as performing an interaction test for each variable in the study for identification of important baseline factors, the approach controlling the overall type I error is not practical during the biomarker discovery stage. For example, with 1,000 genomic variables, the significance level for each individual test should be set at 0.00005 in order to ensure 5% overall error rate. This criterion is very stringent and can result in very few or no significant biomarker variables being selected. False discovery rate (FDR) is an alternative error measure commonly used in multiple testing when the number of tests is large (47-52), mostly in the discover stage. The FDR approach considers the proportion of significant findings over the total number of significant findings. For example, if 20 biomarkers are declared as significant, a FDR of 5% implies that there can be 1 or fewer false positive out of the 20 significant results. The FDR approach allows the findings to be made, provided that the investigator is willing to accept a small fraction of false positive findings. Since predictive biomarkers are used to identify biomarker-positive patients, a small fraction of false positive biomarkers may not have a serious impact on classifier performance. FDR can be applied to the first stage gene feature selection of the ASD. Sometimes, the comparison-wise error rate with a pre-specified fixed significance level is used to select interesting gene features that interact with the treatment.
Imbalanced subgroup size
One frequent problem encountered in subgroup identification is that subgroup sizes may differ considerably. That is, the number in the biomarker-positive patients is much smaller than the number in the biomarker-negative patients, or vice versa. When the subgroup sizes are very different, most standard binary classifiers would give high accuracy in predicting the majority (large) subgroup and poor accuracy in predicting the minority (small) subgroup. This can result in an erroneous conclusion of subgroup effect and lead to inappropriate treatment selection. Lin and Chen (53) reviewed several algorithms for classification of imbalanced class size data and correction strategies to improve accuracy in minority group prediction. They evaluated the three commonly used algorithms: DLDA (33), RF (30), and SVM (31,32). They showed that the standard DLDA algorithm performed reasonable well if the total sample size is reasonable large. All three algorithms can be improved by incorporating an ensemble algorithm (53,54). In particular, the DLDA has been shown to perform well in the analysis of genomic data (25) and is robust against imbalanced data (53) without incorporating correction strategy.
Power and sample size
In designing a clinical trial, sample size must be estimated to ensure a high probability of having a significant test result, if indeed there is a treatment effect. In a typical trial, sample size estimation depends on: (I) the level of significance α, (II) the desired probability to detect treatment effect (1-β), and (III) targeted effect size (ES) for the treatment effect (the smallest different or ratio between treatment and control arms). For example, setting α =5% and (1-β) =80%, if the background probability of response for the control arm is 0.4 and the targeted probability of response for the treatment arm is 0.6 (ES =0.2), then the needed sample size is 97 per arm. The needed sample size is 145 per arm with α =1%.
In subgroup analysis, needed sample size to assess subgroup treatment effect will likely be much larger. First, if the prevalence for the biomarker-positive subgroup is 50%, then the needed sample size will be double per arm. More samples are needed if the prevalence for the subgroup is smaller. Second, prior to conducting subgroup analysis, subgroups need to be identified. This step involves interaction test to identify predictive biomarkers. Unfortunately, sample size determination for subgroup analyses has not been well studied. The needed sample size for the interaction test is much larger than the needed sample size to assess a treatment effect (53). Furthermore, the interaction test needs to be performed for each genomic variable. The level of significance needs to be adjusted to account for multiple testing. Third, the binary classifier to identify a biomarker positive subgroup would have misclassification error; there might be both false positive and false negative errors that would affect the power of testing subgroup treatment effect. Finally, the ASD (20) and cross-validated ASD (37) two-stage approach used only a fraction of samples to validate treatment effect. The performance of the cross-validated ASD (37) also depended on the choice of the two threshold parameters R and G. In general, when the proportion of the biomarker positive subgroup is small, say, 10% or less, to ensure sufficient power to observe a sufficient number of treatment responses so that biomarker positive subgroup can be identified, sample size not only depends on the overall effect size, but, also true effect size in the biomarker positive subgroup, which are unknown. Further studies on the sample size and power in the context of adaptive clinical trial designs for treatment selection would be worthwhile.
Validation of predictive classifiers
Biomarker classifiers are typically developed using available samples from a single trial. A predictive classifier developed from a single study does not reflect many sources of variability outside research conditions, such as historical, geographic, methodologic, spectrum, and follow-up interval aspects (55,56). Validation of a classifier developed from a single data source does not account for potential sources of variation encountered in clinical applications. There are studies showing that several published lung cancer biomarkers were not reproducible (57-62). For example, several lung cancer studies have identified biomarker signatures associated with survival outcomes in their original discovery datasets; however, a study has shown that the largest number of overlapping predictive biomarkers between two independent studies was only four, and most often even zero (63). The lack of reproducibility would be difficult to justify to conduct a clinical trial. In evaluation of a classifier, two most important considerations (53) are (I) predictability—ability to accurately identify biomarker positive patients; and (II) generalizability—ability to predict samples generated from different batches (different locations or times). The term “generalizability” includes the meaning of “reproducibility” (ability to reproduce the performance) and “transportability” (ability to accurately classify similar data generated from different experimental conditions). The term “reproducibility” is a terminology commonly used in the evaluation of different platforms, studies, gene signatures, etc(64,65). Assessment of reproducibility of a classifier within a study is referred to as an internal validation, and across studies is as an external validation.
In theory, some classifiers may have good predictability but poor reproducibility, or vice versa. However, predictability appears to be a necessary condition for a classifier to have good reproducibility. Classifiers with high predictability and reproducibility are obviously desirable. A predictive classifier should perform well in both predictability and reproducibility. To completely validate a predictive classifier, more than one retrospective and prospective trial may be needed. Predictive classifier should be internally and externally validated prior to clinical validation.
For survival outcomes, the predictive scores are estimated before assigning a threshold cutoff to define biomarker-positive and biomarker-negative patients. The predictive scores are derived from the weighted sum of predictive biomarker values ∑ wj xj. The predictive scores represent the relative rankings of patients’ survival probability in the control and treatment arms. There are several measures and methods for the evaluation of the estimated predictive scores (34). These measures primarily evaluate agreement between the predictive scores and the observed survival times. They include the concordance index (66-68), Brier scores (69), log-rank P value and several others (70-73). A prediction model should have a high concordance score before determining the threshold cutoff to classify positive and negative biomarker subgroups.
Adaptive clinical trial design is used not only to validate a predictive biomarker classifier, but also to optimize treatment selection. Validation of a biomarker adaptive design involves: (I) evaluation of the “accuracies” of the classifier in patient classification; and (II) evaluation of treatment effect in the biomarker positive subgroup identified by the classifier. Ideally the classifier should have high sensitivity and specificity, at least 95% or higher, and hence high accuracy. Performance of a classifier depends on the prevalence proportion, sample size, and the biomarker set identified. It is worth mentioning that for prediction problems, the omission of biomarkers (false negatives) would have more serious impact on accuracy than the inclusion of non-biomarkers (false positives) in the classifier. The FDR approach uses a less stringent criterion to select potential predictive biomarkers, it should be a appropriate error measure for the interaction test to identify predictive biomarkers.
The ASD was proposed as a supplementary test when the test for overall treatment effect is not significant. For ASD, a reduced significance level at 4% (instead of 5%) for the overall treatment effect and 1% for the subgroup effect has been suggested. The 5% type I error rate can be allocated in various ways for the two analyses. Scher et al. (22) suggested using 1% or 2% significance level for the overall effect and 4% or 3% for the subgroup effect since the sample size in the subgroup is smaller. Reducing the significance level requires an increase of the trial sample size. Furthermore, the power of the subgroup test depends greatly on the prevalence proportion and the effect size in the specific subgroup of interest. In general, a larger sample size is often needed in an ASD design if detection of the subgroup effect is of primary interest and the effect size in the subgroup is not large.
Example: analysis of a synthetic dataset
An in silico experiment was conducted to illustrate development of a biomarker adaptive design in a two-arm control and treatment study. The number of patients per arm was 200; the proportion of the biomarker positive subgroup was 0.1. The probability of response for all patients in the control arm was 0.2, the probability of response was 0.2 for the biomarker negative subgroup and the probability was 0.6 for the biomarker positive subgroup. The total number of genomic variables was 5,000, among which there were 10 predictive biomarkers. The genomic variables were generated from an independent normal distribution with mean 0 for the non-predictive biomarkers and with mean 1.791 for the predictive biomarkers. The standard deviation was 0.3 for all genomic variables.
A typical observed dataset was analyzed for illustration. Each arm had 20 (10%) biomarker positive patients and 180 (90%) biomarker negative patients. The total number of biomarker positive patients is 40 and the total number of biomarker negative patients is 360. From the control arm, the observed positive responses were 3 and 30 for the positive and negative subgroups, respectively; from the treatment arm, the observed positive responses were 15 and 36 for the positive and negative subgroups, respectively. The analyses performed 10-fold and 2-fold cross validation using the DLDA classification algorithm and the MLV method of ASD. The level of significance in the interaction test was set at 0.005. For the 10-fold cross validation, the average number of significant genes identified was 12.4, of which 9.1 were truly predictive biomarkers. For the 2-fold cross validation, the average number of significant genes identified were 3.5, of which 1.5 were truly predictive biomarkers.
The analyses focused on comparison of the two classifiers to identify biomarker positive patients. Two main considerations in the evaluation are: (I) the sensitivity and specificity of the classifiers and (II) the power of the subgroup test. The MLV procedures require pre-specification of the two parameters R and G; we considered ln(R) = 1, 2 and G = 2, 3. These four cases cover the best choices for the two parameters. Table 1 shows the performance of the two classifiers. The 10-fold cross validation approach shows much better performance than the 2-fold cross validation approach. In the MLV method, a small value of ln(R) or G represents a mild tuning parameter to select biomarker positive patients resulting in higher sensitivity and lower specificity.
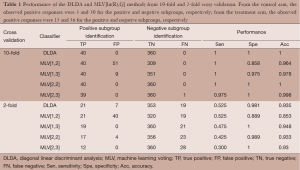
Full table
In 10-fold cross validation, both DLDA and MLV[2,2] correctly identified all biomarker positive and negative patients. MLV[1,2] correctly identified 40 biomarker positive patients (high sensitivity), but it also incorrectly identified 51 biomarker negative patients as biomarker positives (low specificity). Table 2 shows the P values of the subgroup test on the biomarker positive patients identified by the two classifiers. In 10-fold cross validation, both DLDA and MLV[2,2] correctly identified all 20 biomarker positive patients in each arm. The 20 patients included all 3 positive outcomes in the control arm and all 15 positive outcomes in the treatment arm. The P value of the subgroup test was 0.0003. MLV[1,2] identified 91 biomarker positive patients, 63 from the control arm and 28 from the treatment arm. Among of the 63 patients in the control arm, 25 showed positive outcomes, but only 3 were biomarker positive patients. Among the 28 patients in the treatment arm, 18 showed positive outcomes of which 15 were biomarker positive patients. The subgroup test for biomarker negative patients was not significant.
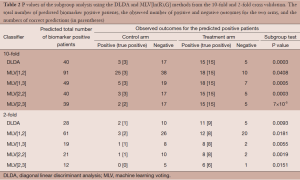
Full table
In this analysis, the number of patients per arm was n=200, and the proportion of biomarker positive subgroup was P=0.10. Denote uij as the response probability for the i-th subgroup (i =0 for biomarker negative and i =1 for biomarker positive) in the j-th arm (j =0 for control and j =1 for treatment). The analysis considered u00 = u01 = u10 =0.2, and u11 =0.6. The performance of a biomarker adaptive design depends on n, p, u00, u01, u10, and u11. Further simulation for various combinations of these parameters will be helpful in the development of biomarker adaptive design for that analysis of subgroup effects.
Discussion
Development of predictive biomarkers remains challenging in clinical trials. Over a decade, only a very limited number of genomic signatures/biomarkers move forward to clinical practices. Many factors contribute to such slow progress; a main reason is that genomic data analysis is considered as an exploratory objective for hypothesis generating due to the complexity of the high-dimensional nature and generally without well-defined clinical hypotheses. The ASD attempts to address this issue by integrating the signature development into the primary objective for phase III randomized trials. This strategy sheds new light on plausible use of genomic biomarkers as a trial objective. However, vigorous statistical methodology is needed to achieve this goal. In this review, we present the key steps in the development of predictive biomarkers to assess treatment effect and discuss statistical issues encountered in the development of a biomarker adaptive design for clinical trials. This involves a statistical test for the interaction effect model to identify potentially useful biomarkers to classify patients into subgroups. It is worth noting again that the biomarker identification and patient subgroup classification were developed sequentially in a single trial. In a clinical trial dataset involving high dimensional genomic variables, such as gene expression data, whole genome scanning data, next generation sequencing data, the number of subjects studied is often far less than the number of genomic variables due to financial feasibility. There can be multiple biomarker classifiers that are similarly plausible with comparable performances. There are several challenges in both biomarker identification and classifier development.
One major challenge is multiplicity in biomarker classifier development. Here, multiplicity does not refer to hypothesis testing, but to the selection among multiple plausible predictive models. However, some may argue that the multiplicity in biomarker classifier development is irrelevant as long as a responsive patient subset can be identified. Due to the empirical nature of classifier development, the predictive models are governed by the pre-specified tuning parameter sets if, for example, an ASD classifier is considered. Wang and Li (38) showed that the unknown true treatment effect size in the biomarker positive patient and the clinical utility of a biomarker classifier play important roles in the ability to identify a ‘good’ biomarker classifier. In the absence of true effect sizes, it is worth noting that there may be no clearly predictable relationship between the choices of the tuning parameters and the ability to demonstrate treatment effect in the biomarker positive subset when the unknown true treatment effect size is not large in the biomarker positive patients, see scenario V in (38).
Another major challenge for ASD biomarker development in a controlled clinical trial is the availability of an in vitro diagnostic assay mid-trial (23) or at trial completion (36) when a biomarker classifier is only developed through an empirical algorithm. In such cases, the actual diagnostic assay containing just the selected gene features may only be feasibly available after the details of the biomarker classifier are fully developed. It is challenging to argue that the actual diagnostic assay is already analytically validated at the time it is to be used to classify patients and to test treatment effect either in all patients or in the positively classified patients in one trial. This bears the question about the biomarker classification accuracy, or its PPV and NPV applying to specific subgroups, one positively classified and one negatively classified, which will impact the test result of treatment effect in the biomarker positive patient subgroup.
A third major challenge is how to reconcile the statistical testing of a subgroup effect hypothesis while exploring the existence of a biomarker classifier potentially predictive of treatment effect as confirmatory and unambiguous? The issue of a viable in vitro diagnostic assay has been mentioned previously. The ASD design attempts to identify a positive subgroup via a pre-specified two-step process (38) should the test of treatment effect in all patients does not achieve statistical significance based on a pre-specified test level. In addition, the identification of the biomarker positive subgroup relies on the pre-specified choices of R and G during the development stage.
Pre-specification of a biomarker subgroup hypothesis in the ASD approach is a useful tool to generate a clinical hypothesis of a biomarker classifier that may be predictive of treatment effect, which assesses the treatment effect in the biomarker classifier defined subgroup either using the second stage data alone (21) or via internal cross validation (37) when needed. The pre-specified algorithm does not necessarily guarantee the existence of a true predictive biomarker during biomarker development. Treatment effect in the biomarker defined negative subgroup may not be formally evaluated with an ASD approach. The issues should be equally applicable with DLDA, MLA or any other types of prediction algorithm used in the two-step process similarly defined to test treatment effects for all patients and for the biomarker positive patients within the same confirmatory trial.
Acknowledgments
The views presented in this paper are those of the authors and do not necessarily represent those of the U.S. Food and Drug Administration.
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the editorial office, Translational Cancer Research for the series “Statistical and Bioinformatics Applications in Biomedical Omics Research”. The article has undergone external peer review.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2014.05.04). The series “Statistical and Bioinformatics Applications in Biomedical Omics Research” was commissioned by the editorial office without any funding or sponsorship. DTC served as the unpaid Guest Editor of the series and serves as an unpaid editorial board member of Translational Cancer Research. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Nesbitt JC, Putnam JB Jr, Walsh GL, et al. Survival in early-stage non-small cell lung cancer. Ann Thorac Surg 1995;60:466-72. [PubMed]
- Hoffman PC, Mauer AM, Vokes EE. Lung cancer. Lancet 2000;355:479-85. [PubMed]
- Subramanian J, Simon R. Gene expression-based prognostic signatures in lung cancer: ready for clinical use? J Natl Cancer Inst 2010;102:464-74. [PubMed]
- Balis FM. Evolution of anticancer drug discovery and the role of cell-based screening. J Natl Cancer Inst 2002;94:78-9. [PubMed]
- Schilsky RL. End points in cancer clinical trials and the drug approval process. Clin Cancer Res 2002;8:935-8. [PubMed]
- Rothenberg ML, Carbone DP, Johnson DH. Improving the evaluation of new cancer treatments: challenges and opportunities. Nat Rev Cancer 2003;3:303-9. [PubMed]
- Biomarkers Definitions Working Group. Biomarkers and surrogate endpoints: preferred definitions and conceptual framework. Clin Pharmacol Ther 2001;69:89-95. [PubMed]
- Lassere MN, Johnson KR, Boers M, et al. Definitions and validation criteria for biomarkers and surrogate endpoints: development and testing of a quantitative hierarchical levels of evidence schema. J Rheumatol 2007;34:607-15. [PubMed]
- Jenkins M, Flynn A, Smart T, et al. A statistician’s perspective on biomarkers in drug development. Pharm Stat 2011;10:494-507. [PubMed]
- Buyse M, Michiels S, Sargent DJ, et al. Integrating biomarkers in clinical trials. Expert Rev Mol Diagn 2011;11:171-82. [PubMed]
- Wang SJ. Biomarker as a classifier in pharmacogenomics clinical trials: a tribute to 30th anniversary of PSI. Pharm Stat 2007;6:283-96. [PubMed]
- Mizuarai S, Irie H, Kotani H. Gene expression-based pharmacodynamic biomarkers: the beginning of a new era in biomarker-driven anti-tumor drug development. Curr Mol Med 2010;10:596-607. [PubMed]
- Fleming TR, DeMets DL. Surrogate end points in clinical trials: are we being misled? Ann Intern Med 1996;125:605-13. [PubMed]
- Baker SG, Kramer BS. A perfect correlate does not a surrogate make. BMC Med Res Methodol 2003;3:16. [PubMed]
- Weir CJ, Walley RJ. Statistical evaluation of biomarkers as surrogate endpoints: a literature review. Stat Med 2006;25:183-203. [PubMed]
- Sargent DJ, Conley BA, Allegra C, et al. Clinical trial designs for predictive marker validation in cancer treatment trials. J Clin Oncol 2005;23:2020-7. [PubMed]
- Mandrekar SJ, Sargent DJ. Clinical trial designs for predictive biomarker validation: theoretical considerations and practical challenges. J Clin Oncol 2009;27:4027-34. [PubMed]
- Wang SJ, O’Neill RT, Hung HM. Approaches to evaluation of treatment effect in randomized clinical trials with genomic subset. Pharm Stat 2007;6:227-44. [PubMed]
- Mandrekar SJ, Sargent DJ. Clinical trial designs for predictive biomarker validation: one size does not fit all. J Biopharm Stat 2009;19:530-42. [PubMed]
- Freidlin B, Simon R. Adaptive signature design: an adaptive clinical trial design for generating and prospectively testing a gene expression signature for sensitive patients. Clin Cancer Res 2005;11:7872-8. [PubMed]
- Wang SJ, Hung HM, O’Neill RT. Adaptive patient enrichment designs in therapeutic trials. Biom J 2009;51:358-74. [PubMed]
- Scher HI, Nasso SF, Rubin EH, et al. Adaptive clinical trial designs for simultaneous testing of matched diagnostics and therapeutics. Clin Cancer Res 2011;17:6634-40. [PubMed]
- US FDA. Draft Drug Diagnostic Co-Development Preliminary Concept Paper. Available online: http://www.fda.gov/downloads/drugs/scienceresearch/researchareas/pharmacogenetics/ucm116689.pdf
- US FDA. In Vitro Companion Diagnostic Devices. Available online: http://www.fda.gov/medicaldevices/deviceregulationandguidance/guidancedocuments/ucm262292.htm
- Baek S, Tsai CA, Chen JJ. Development of biomarker classifiers from high-dimensional data. Brief Bioinform 2009;10:537-46. [PubMed]
- McCullagh P, Nelder JA. eds. Generalized Linear Model, 2nd Edition. London: Chapman Hall, 1989.
- Cox DR, Oakes D. eds. Analysis of survival data. London: Chapman Hall/CRC, 1984.
- Lee JW, Lee JB, Park M, et al. An extensive comparison of recent classification tools applied to microarray data. Comput Stat Data An 2005;48:869-85.
- Moon H, Ahn H, Kodell RL, et al. Ensemble methods for classification of patients for personalized medicine with high-dimensional data. Artif Intell Med 2007;41:197-207. [PubMed]
- Breiman L. Random forest. Mach Learn 2001;45:5-32.
- Vapnik V. eds. The Nature of Statistical Learning Theory. New York: Springer, 1995.
- Guyon I, Weston J, Barnhill S, et al. Gene selection for cancer classification using support vector machines. Mach Learn 2002;46:389-422.
- Dudoit S, Fridlyand J, Speed T. Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc 2002;97:77-87.
- Chen HC, Kodell RL, Cheng KF, et al. Assessment of performance of survival prediction models for cancer prognosis. BMC Med Res Methodol 2012;12:102. [PubMed]
- Chen DT, Hsu YL, Fulp WJ, et al. Prognostic and predictive value of a malignancy-risk gene signature in early-stage non-small cell lung cancer. J Natl Cancer Inst 2011;103:1859-70. [PubMed]
- Jiang W, Freidlin B, Simon R. Biomarker-adaptive threshold design: a procedure for evaluating treatment with possible biomarker-defined subset effect. J Natl Cancer Inst 2007;99:1036-43. [PubMed]
- Freidlin B, Jiang W, Simon R. The cross-validated adaptive signature design. Clin Cancer Res 2010;16:691-8. [PubMed]
- Wang S, Li MC. Impacts of predictive genomic classifier performance on subpopulation-specific treatment effects assessment. Stat Biosci 2014. doi:
10.1007/s12561-013-9092-y . - Brookes ST, Whitely E, Egger M, et al. Subgroup analyses in randomized trials: risks of subgroup-specific analyses; power and sample size for the interaction test. J Clin Epidemiol 2004;57:229-36. [PubMed]
- Pocock SJ, Hughes MD, Lee RJ. Statistical problems in the reporting of clinical trials. A survey of three medical journals. N Engl J Med 1987;317:426-32. [PubMed]
- Yusuf S, Wittes J, Probstfield J, et al. Analysis and interpretation of treatment effects in subgroups of patients in randomized clinical trials. JAMA 1991;266:93-8. [PubMed]
- Assmann SF, Pocock SJ, Enos LE, et al. Subgroup analysis and other (mis)uses of baseline data in clinical trials. Lancet 2000;355:1064-9. [PubMed]
- Song Y, Chi GY. A method for testing a prespecified subgroup in clinical trials. Stat Med 2007;26:3535-49. [PubMed]
- Millen BA. A statistical framework for decision making in confirmatory multipopulation tailoring clinical trials. Drug Inf J 2012;46:647-56.
- Wang SJ, Hung HM. A regulatory perspective on essential considerations in design and analysis of subgroups when correctly classified. J Biopharm Stat 2014;24:19-41. [PubMed]
- Marcus R, Peritz E, Gabriel K. On closed testing procedure with special reference to ordered analysis of variance. Biometrika 1976;63:655-60.
- Benjamin Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Roy Stat Soc B 1995;57:289-300.
- Benjamin Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Anna Stat 2001;29:1165-88.
- Storey J. A direct approach to false discovery rates. J Roy Stat Soc B 2002;64:479-98.
- Tsai CA, Hsueh HM, Chen JJ. Estimation of false discovery rates in multiple testing: application to gene microarray data. Biometrics 2003;59:1071-81. [PubMed]
- Polley MY, Freidlin B, Korn EL, et al. Statistical and practical considerations for clinical evaluation of predictive biomarkers. J Natl Cancer Inst 2013;105:1677-83. [PubMed]
- Chen JJ, Roberson PK, Schell MJ. The false discovery rate: a key concept in large-scale genetic studies. Cancer Control 2010;17:58-62. [PubMed]
- Lin WJ, Chen JJ. Class-imbalanced classifiers for high-dimensional data. Brief Bioinform 2013;14:13-26. [PubMed]
- Chen JJ, Tsai CA, Young JF, et al. Classification ensembles for unbalanced class sizes in predictive toxicology. SAR QSAR Environ Res 2005;16:517-29. [PubMed]
- Justice AC, Covinsky KE, Berlin JA. Assessing the generalizability of prognostic information. Ann Intern Med 1999;130:515-24. [PubMed]
- Chen HC, Chen JJ. Assessment of reproducibility of cancer survival risk predictions across medical centers. BMC Med Res Methodol 2013;13:25. [PubMed]
- Ramaswamy S, Ross KN, Lander ES, et al. A molecular signature of metastasis in primary solid tumors. Nat Genet 2003;33:49-54. [PubMed]
- Bhattacharjee A, Richards WG, Staunton J, et al. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. Proc Natl Acad Sci U S A 2001;98:13790-5. [PubMed]
- Liu J, Blackhall F, Seiden-Long I, et al. Modeling of lung cancer by an orthotopically growing H460SM variant cell line reveals novel candidate genes for systemic metastasis. Oncogene 2004;23:6316-24. [PubMed]
- Blackhall FH, Wigle DA, Jurisica I, et al. Validating the prognostic value of marker genes derived from a non-small cell lung cancer microarray study. Lung Cancer 2004;46:197-204. [PubMed]
- Parmigiani G, Garrett-Mayer ES, Anbazhagan R, et al. A cross-study comparison of gene expression studies for the molecular classification of lung cancer. Clin Cancer Res 2004;10:2922-7. [PubMed]
- Lu TP, Chuang EY, Chen JJ. Identification of reproducible gene expression signatures in lung adenocarcinoma. BMC Bioinformatics 2013;14:371. [PubMed]
- Lau SK, Boutros PC, Pintilie M, et al. Three-gene prognostic classifier for early-stage non small-cell lung cancer. J Clin Oncol 2007;25:5562-9. [PubMed]
- Shi L, Reid LH, Jones WD, et al. The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nat Biotechnol 2006;24:1151-61. [PubMed]
- Chen JJ, Hsueh HM, Delongchamp RR, et al. Reproducibility of microarray data: a further analysis of microarray quality control (MAQC) data. BMC Bioinformatics 2007;8:412. [PubMed]
- Harrell FE Jr, Califf RM, Pryor DB, et al. Evaluating the yield of medical tests. JAMA 1982;247:2543-6. [PubMed]
- Kattan MW. Evaluating a new marker’s predictive contribution. Clin Cancer Res 2004;10:822-4. [PubMed]
- Newson R. Confidence intervals for rank statistics: Somers’ D and extensions. Stata J 2006;6:309-34.
- Gerds TA, Schumacher M. Consistent estimation of the expected Brier score in general survival models with right-censored event times. Biom J 2006;48:1029-40. [PubMed]
- Bair E, Tibshirani R. Semi-supervised methods to predict patient survival from gene expression data. PLoS Biol 2004;2:E108 [PubMed]
- Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics 2000;56:337-44. [PubMed]
- Schemper M. Predictive accuracy and explained variation. Stat Med 2003;22:2299-308. [PubMed]
- Schemper M. The relative importance of prognostic factors in studies of survival. Stat Med 1993;12:2377-82. [PubMed]


