
Factors associated with de novo metastatic disease in invasive breast cancer: comparison of artificial neural network and logistic regression models
Introduction
Breast cancer is the most frequently diagnosed cancer and the leading cause of cancer death among females worldwide, with an estimated 1.7 million cases and 521,900 deaths in 2012 (1). With advancement of imaging technology, early detection rate of breast cancer has gradually risen but approximately 2.4–6% of patients are still initially being diagnosed as de novo stage IV breast cancer (2,3). This subgroup, called de novo metastatic breast cancer, can be viewed as a prognostic subgroup that is distinct from those with recurrent metastasis (4). Previous data indicate that median survival of those with metastatic breast cancer ranges between 18 and 24 months (5). The pattern of site-specific metastases is similar in patients with de novo stage IV breast cancer, whose most common metastatic sites were bone, followed by lung, liver, and brain (6).
There are quite a number of studies exploring risks involved in long term survival of metastatic breast cancer patients (7,8), while few focuses on occurrence of de novo metastatic breast cancer. Therefore, here we attempted to construct population-based models in order to clarify factors concerning occurrence of de novo metastatic breast cancer.
The traditional statistic model, logistic regression (LR) has been one of the most commonly applied predictive models in medicine and allows intuitive interpretation in its model structure (9). While Warren McCulloch and Walter Pitts created a computational model for neural networks based on mathematics and algorithms called threshold logic in 1943 (8), paving the way for artificial neural network (ANN). Compared to LR, ANN owns a more flexible structure and is possibly capable to discover more implicit interactions and complex connections throughout input variables (10). Both approaches have been used with success in predicting and estimating clinical results in various kinds of diseases, such as cancer and cardiovascular disease, etc. (11,12). We were wondering which model would be more suitable for solving such a complex clinical issue as de novo metastasis of breast cancer. Therefore, we compared LR and ANN models, to further illustrate their application in clinical practice in this study.
Methods
Data source
This study is cross sectional. Data were obtained from a total of 18 cancer registries utilizing the National Cancer Institute’s Surveillance, Epidemiology and End Results (SEER) Cancer database released April 2017, based on the November 2016 submission (www.seer.cancer.gov) through SEER-stat software (SEER Stat 8.3.4). Cases that met the following criteria were included: (I) female patients diagnosed with invasive breast cancer in 2010 (the distant metastasis status was recorded from 2010 on); (II) breast cancer as the first and only malignant tumor. Patients in tumor stage of T0 or Tis were excluded. Finally, 40,899 eligible patients were enrolled.
Data preparation
Data collected for each patient included patient demographics and tumor characteristics. TNM and clinical stages were restaged according to the 7th American Joint Committee on Cancer’s (AJCC) Staging Manual (13). Invasive breast cancers were classified into seven histological types including invasive ductal carcinoma, invasive lobular carcinoma, invasive tubular carcinoma, invasive mixed carcinoma, invasive mucinous carcinoma, other invasive carcinomas and Paget’s disease, as suggested by Gathani et al. (14).
The review of published papers and counseling consulting with oncologists were performed to determine input variables for metastasis modeling (15). Totally, race, histology, primary site, tumor grade, laterality, regional lymph nodes status, tumor size, ER status, PR status, Her-2 status, Bloom-Richardson (Nottingham) score, number of positive ipsilateral axillary lymph nodes and lymph node ratio (LNR) were integrated as input variables. T stage of those with distant metastasis were all unknown, which led to complete separability of the data, therefore it was not taken as an input variable. For handling missing values of quantitative variables as number of positive ipsilateral axillary lymph nodes, Bloom-Richardson (Nottingham) score and LNR, simple mean imputation was adopted. Dependent variable was a binary variable that 1 and 0 represented metastasis and non-metastasis respectively.
Data mining
Constructing LR model
Generally, LR inspects the linear relation between input variables and the log-odds of the event presence probability p, i.e.,
Log [p/(1−p)] = β0 + β1X1 + … + βnXn.
We used a modified 10-fold cross-validation approach to construct LR models (16). The process as the following steps was illustrated as in Figure 1: (I) data was splitted into 90% train set and 10% test set in a random way; (II) constructed a multivariate LR model fitted on the train set with continuous variables (i.e., tumor size, Bloom-Richardson (Nottingham) score, number of positive ipsilateral axillary lymph nodes, LNR) treated continuously and discrete variables (i.e., race, histology, primary site, tumor grade, laterality, regional lymph nodes status, ER status, PR status, Her-2 status) treated categorically; (III) model was validated on the test set and a predicted value >0.5 was taken as 1 otherwise 0; (IV) performance of model was evaluated on the test set with sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), accuracy as well as area under ROC curve (AUC) using pROC package available in R; (V) steps 1–4 were repeated 10 times, eventually getting an evaluation indexes series of 10.
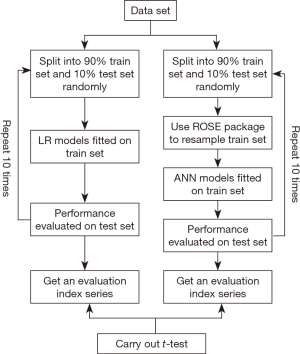
Constructing ANN model
A representative ANN comprises three layers: input nodes in the input layer representing each input variable Xi, respectively; a single output node in the output layer standing for the outcome possibility p; and hidden layers connecting input and output layers, where hidden nodes contain network’s intermediate values but do not have any physical meaning or explicit interpretation.
Since the value of dependent variable were not balanced and non-metastasis count was nearly 17 times of that of metastasis, the learning process of a neural network usually is biased towards classes with majority populations (17). What’s more, balancing class prevalence before training a classifier does not across-the-board improve classifier performance. Whereas, balancing classes is contraindicated for LR models (18). The process was illustrated as in Figure 1: (I) data was splitted into 90% train set and 10% test set in a random way; (II) used method of “both” in ROSE package available in R to oversample the minority class and undersample the majority class in the train set; (III) constructed a simple feed forward neural network using neuralnet package available in R fitted on the resampled train set; (IV) model was validated on the test set and a predicted value >0.5 was taken as 1 otherwise 0; (V) performance of model was evaluated on the test set with sensitivity, specificity, PPV, NPV, accuracy as well as AUC using pROC package available in R; (V) steps 1–4 were repeated 10 times, eventually getting an evaluation indexes series of 10. Importance of variable in ANN was calculated using Garson’s algorithm in NeuralNetTools package available in R (19).
Comparison of LR and ANN models
Finally, t-tests on the evaluation indexes series including sensitivity, specificity, PPV, NPV, accuracy as well as AUC were carried out to detect difference of efficiency between two kinds of model.
Statistics
All statistical tests were two tailed, where a P value <0.05 was considered statistically significant. All data mining steps were performed using R version 3.0.0 (R Foundation for Statistical Computing, Vienna, Austria).
Results
Patient characteristics
Table 1 summarizes the clinical characteristics of the total 40,899 cases enrolled in the study. The percentages of metastasis and non-metastasis was 5.6% and 94.4% respectively. The two groups were imbalanced on clinical characteristics distribution. Patients with de novo distant metastasis have a tendency of poorer tumor grade (36.9% vs. 32%, P<0.001 for poorly differentiated and undifferentiated), more lymph node invasion (66% vs. 30.2%, P<0.001 for N1, N2 and N3), less ER(+) (64.8% vs. 77.9%, P<0.001), less PR(+) (49.8% vs. 66.6%, P<0.001), more Her-2(+) (19.6% vs. 13.8%, P<0.001), larger tumor size (42.48±38.11 vs. 22.38±26.03 mm, P<0.001), higher Bloom-Richardson (Nottingham) score (6.53±1.18 vs. 6.31±1.53, P<0.001), more invasion of ipsilateral axillary lymph nodes (2.19±4.02 vs. 1.17±3.07, P<0.001) and higher LNR (0.24±0.28 vs. 0.11±0.21, P<0.001).
Table 1
| Variables | Non-metastasis (N=38,617) | Metastasis (N=2,282) | P value# |
|---|---|---|---|
| Race | <0.001 | ||
| White | 30,653 (79.4) | 1,727 (75.7) | |
| Black | 4,128 (10.7) | 374 (16.4) | |
| Asian | 3,539 (9.2) | 175 (7.7) | |
| Unknown | 297 (0.8) | 6 (0.3) | |
| Histology | <0.001 | ||
| Invasive ductal carcinoma | 30,272 (78.4) | 1,472 (64.5) | |
| Invasive lobular carcinoma | 3,475 (9.0) | 254 (11.1) | |
| Invasive tubular carcinoma | 248 (0.6) | 0 (0.0) | |
| Invasive mixed ductal, lobular carcinoma | 2,238 (5.8) | 93 (4.1) | |
| Mucinous carcinoma | 785 (2.0) | 10 (0.4) | |
| Other invasive carcinoma | 1,592 (4.1) | 451 (19.8) | |
| Paget’s disease | 7 (0.0) | 2 (0.1) | |
| Primary site | <0.001 | ||
| Nipple and central portion | 1,966 (5.1) | 138 (6.0) | |
| Upper-inner quadrant | 4,531 (11.7) | 132 (5.8) | |
| Lower-inner quadrant | 2,214 (5.7) | 70 (3.1) | |
| Upper-outer quadrant | 13,114 (34.0) | 483 (21.2) | |
| Lower-outer quadrant | 2,815 (7.3) | 88 (3.9) | |
| Axillary tail | 186 (0.5) | 14 (0.6) | |
| Overlapping | 8,169 (21.2) | 417 (18.3) | |
| Unknown | 5,622 (14.6) | 940 (41.2) | |
| Tumor grade | <0.001 | ||
| Well differentiated | 8,067 (20.9) | 124 (5.4) | |
| Moderately differentiated | 15,694 (40.6) | 697 (30.5) | |
| Poorly differentiated | 12,177 (31.5) | 818 (35.8) | |
| Undifferentiated, anaplastic | 174 (0.5) | 25 (1.1) | |
| Unknown | 2,505 (6.5) | 618 (27.1) | |
| Laterality | <0.001 | ||
| Left side | 19,482 (50.4) | 1,053 (46.1) | |
| Right side | 18,701 (48.4) | 1,069 (46.8) | |
| Bilateral | 9 (0.0) | 22 (1.0) | |
| Unknown | 425 (1.1) | 138 (6.0) | |
| Regional lymph nodes status | <0.001 | ||
| N0 | 24,806 (64.2) | 439 (19.2) | |
| N1 | 8,254 (21.4) | 696 (30.5) | |
| N2 | 2,111 (5.5) | 198 (8.7) | |
| N3 | 1,293 (3.3) | 612 (26.8) | |
| Nx | 2,153 (5.6) | 337 (14.8) | |
| ER status | <0.001 | ||
| Negative | 6,505 (16.8) | 493 (21.6) | |
| Positive | 30,096 (77.9) | 1,478 (64.8) | |
| Borderline | 36 (0.1) | 1 (0.0) | |
| Unknown | 1,980 (5.1) | 310 (13.6) | |
| PR status | <0.001 | ||
| Negative | 10,539 (27.3) | 806 (35.3) | |
| Positive | 25,725 (66.6) | 1,137 (49.8) | |
| Borderline | 114 (0.3) | 9 (0.4) | |
| Unknown | 2,239 (5.8) | 330 (14.5) | |
| Her-2 status | <0.001 | ||
| Negative | 29,313 (75.9) | 1,376 (60.3) | |
| Positive | 5,335 (13.8) | 448 (19.6) | |
| Borderline | 908 (2.4) | 70 (3.1) | |
| Unknown | 3,061 (7.9) | 388 (17.0) | |
| Tumor size (mm) | 22.38±26.03 | 42.48±38.11 | <0.001 |
| Bloom-Richardson (Nottingham) score | 6.31±1.53 | 6.53±1.18 | <0.001 |
| Number of positive ipsilateral axillary lymph nodes | 1.17±3.07 | 2.19±4.02 | <0.001 |
| Lymph node ratio (LNR) | 0.11±0.21 | 0.24±0.28 | <0.001 |
Data are presented as n (%) or mean ± std. #, P value of the difference of categorical variables is calculated by Chi-square test. P value of the difference of continuous variables is calculated by t-test.
LR modeling
When a classification threshold of 0.5 was applied to the test set, the LR models had an average sensitivity of 99.5%, specificity of 16.7%, PPV of 95.4%, NPV of 66.6%, accuracy of 95.0% and AUC of 0.844, respectively (Table 2). When exploring one LR model, almost all of the thirteen independent variables were identified to be significantly correlated with occurrence of distant metastasis (P<0.05) (Table 3). Especially, bilateral vs. left-sided [odds ratio (OR): 16.176, 95% CI: 6.665–43.674, P<0.001], undifferentiated and anaplastic vs. well differentiated (OR: 4.440, 95% CI: 2.474–7.657, P<0.001), and N1 vs. N0 (OR: 4.183, 95% CI: 3.629–4.825, P<0.001) were thought to be strong stimulators for de novo metastasis.
Table 2
| Variable | LR models (mean ± std) | ANN models (mean ± std) |
|---|---|---|
| Sensitivity | 99.5%±0.1% | 83.1%±0.9% |
| Specificity | 16.7%±2.3% | 88.0%±2.9% |
| PPV | 95.4%±0.4% | 99.1%±0.2% |
| NPV | 66.6%±6.6% | 23.7%±1.9% |
| Accuracy | 95.0%±0.4% | 83.4%±0.8% |
| AUC | 0.844±0.011 | 0.917±0.01 |
LR, logistic regression; ANN, artificial neural network; PPV, positive predictive value; NPV, negative predictive value; AUC, area under ROC (receiver operating curve).
Table 3
| Variable | B | S.E. | Sig. | Exp(B) | 95% CI for Exp(B) |
|---|---|---|---|---|---|
| Race: black (contrast: white) | 0.179 | 0.072 | 0.013 | 1.196 | 1.037–1.375 |
| Histology: invasive lobular carcinoma (contrast: invasive ductal carcinoma) | 0.400 | 0.084 | <0.001 | 1.492 | 1.262–1.756 |
| Primary site: upper-outer quadrant (contrast: nipple and central portion) | −0.381 | 0.116 | 0.001 | 0.683 | 0.546–0.861 |
| Tumor grade: undifferentiated, anaplastic (contrast: well differentiated) | 1.491 | 0.287 | <0.001 | 4.440 | 2.474–7.657 |
| Laterality: bilateral (contrast: left side) | 2.783 | 0.473 | <0.001 | 16.176 | 6.665–43.674 |
| Regional lymph nodes status: N1 (contrast: N0) | 1.431 | 0.073 | <0.001 | 4.183 | 3.629–4.825 |
| ER status: ER (+) [contrast: ER(−)] | 0.244 | 0.086 | 0.005 | 1.276 | 1.078–1.509 |
| PR status: PR (+) [contrast: PR(−)] | −0.293 | 0.073 | <0.001 | 0.746 | 0.646–0.862 |
| Her-2 status: Her-2(+) [contrast: Her-2(−)] | 0.245 | 0.069 | <0.001 | 1.278 | 1.114–1.463 |
| Tumor size | 0.006 | 0.001 | <0.001 | 1.006 | 1.005–1.008 |
| Bloom-Richardson (Nottingham) score | −0.083 | 0.025 | <0.001 | 0.921 | 0.878–0.967 |
| Number of positive ipsilateral axillary lymph nodes | −0.165 | 0.011 | <0.001 | 0.848 | 0.830–0.866 |
| Lymph node ratio (LNR) | 0.525 | 0.121 | <0.001 | 1.691 | 1.332–2.136 |
B, coefficient values; S.E., standard error; Sig., significant value; Exp(B), odds ratio; CI, confidence interval.
ANN modeling
As Table 2 shows, an average AUC of 0.917 showed the ANN models fitting well. When the ANN models were applied to the validation set, the average sensitivity, specificity, PPV, NPV, accuracy of models with a classification threshold of 0.5 were listed in Table 2. The results showed a much better PPV than an NPV, that is to say, the ANN model is more suitable to predict metastasis than non-metastasis events, which is also consistent with the clinical needs in real life.
Figure 2 illustrates the structure of the ANN, which is a special classification of a feed forward neural network with one input layer, one hide layer, and one output layer. The input layer consists of thirteen source points of independent variables. The second is a hidden layer containing six nodes. The output layer shows outcome reacting to input patterns. A mapping could be performed from the input space to the hidden space, and then from the hidden space to the output space in this process.
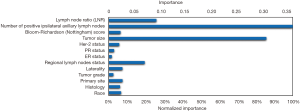
In the training ANN model, we found that among all thirteen independent variables, number of positive ipsilateral axillary lymph nodes, tumor size, LNR and regional lymph nodes status were important factors for metastasis, with normalized importance of 100%, 85.7%, 25.9% and 19.5% respectively (Figure 3).
Comparison between LR and ANN models
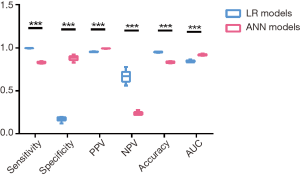
We compared the evaluation indexes of the LR models and ANN models (Figure 4). Although LR models showed significantly higher sensitivity (99.5%±0.1% vs. 83.1%±0.9%, P<0.001), negative predictive value (66.6%±6.6% vs. 23.7%±1.9%, P<0.001) and accuracy (95.0%±0.4% vs. 83.4%±0.8%, P<0.001), the overall AUC value for identifying de novo metastasis using the ANN models was more accurate than the LR models (0.917±0.01 vs. 0.844±0.011, P<0.001). Since AUC is a better measure than accuracy based on formal definitions of discriminancy and consistency (20), we could naturally go to a conclusion that ANN models outperformed traditional LR models in identifying de novo metastasis in invasive breast cancer.
The experiment environment and processing time of these two kinds of model were listed and compared as in Table 4. While under the same experiment environment, ANN models obviously took much longer processing time than LR models did (14,400 vs. 15 minutes for 10-fold cross-validation).
Table 4
| Aspects | LR models | ANN models |
|---|---|---|
| Experiment environment | ||
| System | Windows 7 64-bits | |
| processor | Intel® Core™ i5-6200U CPU @ 2.30 GHz | |
| RAM | 8.00 GB | |
| Software | R version 3.0.0 | |
| Processing time | 15 minutes for 10-fold cross-validation | 14,400 minutes for 10-fold cross-validation |
LR, logistic regression; ANN, artificial neural network.
Discussion
In this study, ANN and LR models were constructed to find out important factors associated with occurrence of de novo metastasis in invasive breast cancer for the first time. We found that ANN model outperformed in identifying de novo metastasis in invasive breast cancer, offering an alternative medical modeling to traditional LR model. In ANN models, number of positive ipsilateral axillary lymph nodes, tumor size, LNR and regional lymph nodes status were important associated factors of de novo metastasis.
De novo metastasis of breast cancer is a complex process involving a number of clinical and individual genetic factors. Patients presenting with de novo metastasis are likely to be different from those with relapsed metastasis in the light of biology and outcomes. Although no significant differences were evident, Kitagawa et al. found the median OS was 46 and 43 months for de novo stage IV disease and relapsed disease, respectively. They also found their prognostic factors differed substantially. Identified prognostic factors were performance status and liver metastasis for de novo stage IV disease, and performance status, hormone receptor status, solitary bone metastasis, and disease-free interval for relapsed disease (21). Former researches that explore relapsed metastasis’ pattern based on molecular subtypes have discovered metastatic spread’s different patterns with notable differences in survival. To some extent, HR+/Her2− tumors predominantly metastasize to the bone while tumors overexpressing Her2 tend to be also found in lung, liver, and brain metastasis (22-24).
Up to now, our study is the first to apply ANN models in clinical practice of exploring occurrence of de novo metastasis of invasive breast cancer with comparison with LR models. LR models revealed that bilateral, undifferentiated and anaplastic tumor, and invasion of lymph nodes were thought to be strong stimulators for metastasis. While ANN models are hard to interpret, we found that number of positive ipsilateral axillary lymph nodes, tumor size, LNR and regional lymph nodes status were primary stimulators. Although the sensitivity, negative predictive value and accuracy were significantly higher in LR model, comparison of AUC showed that ANN model performed more accurately than LR model by approximately 0.073.
As a widely used statistical modeling technique, LR models usually require more formal statistical training to develop. Under such situation, complex nonlinear relationships between dependent and independent variables can't be implicitly detected, therefore they don’t have the ability to detect all possible interactions between predictor variables. However, with the above aspects into consideration, ANN is senior to LR (25,26). As inspired by the human nervous system, ANN is capable of pattern recognition and complex models computation, through which to predict new data outcomes by learning from the past experience. Such capability makes it suitable for prediction tasks and classification in practical situations. Moreover, ANN is inherently non-linear and nonconvex, allowing it more fitting for processing intricate data patterns, as opposed to other conventional techniques that are based on linear methods (27). Since cancer metastasis is such a complicated issue to be forecasted, ANN would be more suitable for such issue although their predicting efficacy is also influenced by model structure of various hidden layers and nodes. It was also manifested by the result that ANN models actually performed better.
However, with the processing time concerned, ANN models would obviously consume much more calculation resources than those traditional regression models, although the processing time will depend on the number of layers and neurons and their involvement in computing the results. Therefore, in order to apply ANN models in highly efficient clinical practice, it is of necessity to equip clinics with adequate computing centers. Furthermore, suitable input variables and reduction of the number of layers and neurons would contribute to improvement of efficiency of models.
There is some limitation in our study. First of all, retrospective studies are inherently biased. In addition, T stage of those with distant metastasis, some data of number of positive ipsilateral axillary lymph nodes, Bloom-Richardson (Nottingham) score and LNR were missing in the dataset.
Conclusions
ANN model outperformed in identifying de novo metastasis in invasive breast cancer, offering an alternative medical modeling to traditional LR model. In ANN models, number of positive ipsilateral axillary lymph nodes, tumor size, LNR and regional lymph nodes status were important associated factors of de novo metastasis. However, much longer processing time of ANN models should also be considered.
Acknowledgments
We sincerely appreciated Yongrui Chen, a candidate PhD on statistics at Chicago University, USA, for his advice on statistics.
Funding: This study was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tcr.2019.01.01). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Torre LA, Bray F, Siegel RL, et al. Global cancer statistics, 2012. CA Cancer J Clin 2015;65:87-108. [Crossref] [PubMed]
- Ruiterkamp J, Ernst MF, de Munck L, et al. Improved survival of patients with primary distant metastatic breast cancer in the period of 1995-2008. A nationwide population-based study in the Netherlands. Breast Cancer Res Treat 2011;128:495-503. [Crossref] [PubMed]
- Siegel RL, Miller KD, Jemal A. Cancer statistics, 2016. CA Cancer J Clin 2016;66:7-30. [Crossref] [PubMed]
- Lobbezoo DJ, van Kampen RJ, Voogd AC, et al. Prognosis of metastatic breast cancer: are there differences between patients with de novo and recurrent metastatic breast cancer? Br J Cancer 2015;112:1445-51. [Crossref] [PubMed]
- Muss HB, Case LD, Richards F 2nd, et al. Interrupted versus continuous chemotherapy in patients with metastatic breast cancer. The Piedmont Oncology Association. N Engl J Med 1991;325:1342-8. [Crossref] [PubMed]
- Wu SG, Li H, Tang LY, et al. The effect of distant metastases sites on survival in de novo stage-IV breast cancer: A SEER database analysis. Tumour Biol 2017;39:1010428317705082. [Crossref] [PubMed]
- Hao Y, Meyer N, Song X, et al. Treatment patterns and survival in metastatic breast cancer patients by tumor characteristics. Curr Med Res Opin 2015;31:275-88. [Crossref] [PubMed]
- Vaz-Luis I, Lin NU, Keating NL, et al. Factors Associated with Early Mortality Among Patients with De Novo Metastatic Breast Cancer: A Population-Based Study. Oncologist 2017;22:386-93. [Crossref] [PubMed]
- Hendriksen JM, Geersing GJ, Moons KG, et al. Diagnostic and prognostic prediction models. J Thromb Haemost 2013;11:129-41. [Crossref] [PubMed]
- Liew PL, Lee YC, Lin YC, et al. Comparison of artificial neural networks with logistic regression in prediction of gallbladder disease among obese patients. Dig Liver Dis 2007;39:356-62. [Crossref] [PubMed]
- Kawakami S, Numao N, Okubo Y, et al. Development, validation, and head-to-head comparison of logistic regression-based nomograms and artificial neural network models predicting prostate cancer on initial extended biopsy. Eur Urol 2008;54:601-11. [Crossref] [PubMed]
- Abedi V, Goyal N, Tsivgoulis G, et al. Novel Screening Tool for Stroke Using Artificial Neural Network. Stroke 2017;48:1678-81. [Crossref] [PubMed]
- Edge SB, Compton CC. The American Joint Committee on Cancer: the 7th edition of the AJCC cancer staging manual and the future of TNM. Ann Surg Oncol 2010;17:1471-4.
- Gathani T, Bull D, Green J, et al. Breast cancer histological classification: agreement between the Office for National Statistics and the National Health Service Breast Screening Programme. Breast Cancer Res 2005;7:R1090-6. [Crossref] [PubMed]
- Marino N, Woditschka S, Reed LT, et al. Breast cancer metastasis: issues for the personalization of its prevention and treatment. Am J Pathol 2013;183:1084-95. [Crossref] [PubMed]
- Little MA, Varoquaux G, Saeb S, et al. Using and understanding cross-validation strategies. Perspectives on Saeb et al. Gigascience 2017;6:1-6. [Crossref] [PubMed]
- Fu X, Wang L, Seng Chua K, et al. editors. Training RBF neural networks on unbalanced data. 9th International Conference on Neural Information Processing (ICONIP'OZ), 2002.
- Zumel N. Does Balancing Classes Improve Classifier Performance? 2015. Available online: http://www.win-vector.com/blog/2015/02/does-balancing-classes-improve-classifier-performance/
- Olden JD, Joy MK, Death RG. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecological Modelling 2004;178:389-97. [Crossref]
- Ling CX, Huang J, Zhang H. AUC: A Better Measure than Accuracy in Comparing Learning Algorithms. In: Xiang Y, Chaib-draa B. editors. Advances in Artificial Intelligence. AI 2003. Lecture Notes in Computer Science (Lecture Notes in Artificial Intelligence), vol 2671. Springer, Berlin, Heidelberg, 2003.
- Kitagawa D, Horiguchi S, Yamashita T, et al. Comparison of outcomes between women with de novo stage IV and relapsed breast cancer. J Nippon Med Sch 2014;81:139-47. [Crossref] [PubMed]
- Gerratana L, Fanotto V, Bonotto M, et al. Pattern of metastasis and outcome in patients with breast cancer. Clin Exp Metastasis 2015;32:125-33. [Crossref] [PubMed]
- Sihto H, Lundin J, Lundin M, et al. Breast cancer biological subtypes and protein expression predict for the preferential distant metastasis sites: a nationwide cohort study. Breast Cancer Res 2011;13:R87. [Crossref] [PubMed]
- Luini A, Aguilar M, Gatti G, et al. Metaplastic carcinoma of the breast, an unusual disease with worse prognosis: the experience of the European Institute of Oncology and review of the literature. Breast Cancer Res Treat 2007;101:349-53. [Crossref] [PubMed]
- Terrin N, Schmid CH, Griffith JL, et al. External validity of predictive models: a comparison of logistic regression, classification trees, and neural networks. J Clin Epidemiol 2003;56:721-9. [Crossref] [PubMed]
- Morteza A, Nakhjavani M, Asgarani F, et al. Inconsistency in albuminuria predictors in type 2 diabetes: a comparison between neural network and conditional logistic regression. Transl Res 2013;161:397-405. [Crossref] [PubMed]
- Pouliakis A, Karakitsou E, Margari N, et al. Artificial Neural Networks as Decision Support Tools in Cytopathology: Past, Present, and Future. Biomed Eng Comput Biol 2016;7:1-18. [Crossref] [PubMed]



