Secondary particle production and physical properties during dose enhancement for spread-out Bragg peaks
Introduction
Rapid developments in radiation therapy technologies have enabled the use of energy of the order of megavoltage or higher, thus reducing the integral dose to surrounding normal tissues. Furthermore, innovative therapies such as image guided radiation therapy and volumetric intensity modulated arc radiotherapy enable the delivery of a tumor-healing dose while lowering the probability of normal tissue complications (1). Radiation therapy using protons relies on the characteristics that energy is not lost in the surface layer when the particles enter the tissue and most of the energy is transferred when the protons reach their maximum range. This type of therapy has been reported to produce a greater dose concentration in tumor tissue and excellent normal tissue protection effects compared to X-rays, the strength of which decrease exponentially with depth (2-4). Thus, radiation therapy is moving from low- to high-energy radiation and developing from X-ray to heavy-particle therapies. The ultimate goal of radiation therapy is to minimize the effects of radiation on surrounding normal tissues while delivering a sufficient healing dose to the tumor. However, special care must be taken because, depending on the position of the tumor, pathologic findings, and body condition, the dose required to improve the tumor control probability (TCP) can cause disorders in normal tissues (5,6). Ideally, the TCP should be high while the normal tissue complication probability (NTCP) remains low, and the difference between them should increase. This concept can be quantified through the therapeutic ratio (TR) (7). To improve the TR, therapies such as concomitant chemoradiotherapy, dose enhancement, hyperthermia, and charged-particle therapy have been developed (8-11). Dose enhancement is a method of increasing the interactive cross-section of materials with a high atomic number and the electron density in the medium, which increases the energy delivered to local sites by increasing the generation of secondary particles such as photoelectrons and Auger electrons (12,13). The radiation physics actions in this process include the photoelectric effect, Compton scattering, and pair production for X-rays; for protons, they can be explained by the Coulomb force between the proton and electron in the material, energy loss by inelastic collision with the nucleus, and so on (14). An increase in cross-section leads to an increase in the linear energy transfer (LET) in the material, which, in turn, increases the relative biological effectiveness, thereby increasing the effectiveness on the tumour (8). Considering biocompatibility and chemical stability, gold, iodine, and gadolinium are used for dose enhancement (15,16). In terms of particle size, the application of nanoparticles has been reported to produce enhanced permeability and retention in the tissue and the vasculature system (17,18). The effect of dose enhancement is influenced by the material type, particle size, concentration, and quality of incident radiation (19). Many studies on this subject have been conducted in recent years, using in vivo and in vitro experiments as well as Monte Carlo simulations.
Most studies on dose enhancement are limited to kilovolt and megavoltage X-rays (20-23), with few studies on dose enhancement related to protons. Therefore, this study analyzed the physical properties of dose enhancement caused by the high-Z materials, and analyzed the changes in secondary particle production caused by the interaction between the enhancement material and the protons.
Methods
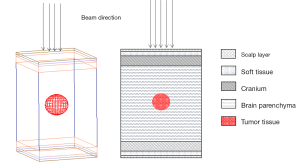
This study used the Geometry and Tracking (Geant4) software ver. 10.03 for Monte Carlo simulations. The head phantom of the medical internal radiation dose (MIRD), developed by the Oak Ridge National Laboratory, the simplified phantom was modeled (24,25). The phantom is composed of a 0.3-cm soft tissue layer, 0.2-cm scalp layer, 11.5-cm parenchyma, 0.9-cm cranium, and 2.5-cm tumor tissue inside the parenchyma (Figure 1). The composition of the materials followed report 46 of the International Commission on Radiation Units and Measurement (ICRU) (see Table 1) (25).
Table 1
| Variable | Density (g/cm3) | A. Density* (atom/b-cm) | H | C | N | O | Na | Mg | P | S | Cl | K | Ca | Fe | Zn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scalp layer | 1.09 | 1.06E−01 | 10.06 | 22.83 | 4.64 | 61.90 | 0.01 | 0.01 | 0.03 | 0.16 | 0.27 | 0.09 | 0.02 | 0.001 | 0.001 |
| Soft tissue | 1.00 | 9.90E−02 | 10.44 | 23.21 | 2.48 | 63.02 | 0.11 | 0.01 | 0.13 | 0.19 | 0.13 | 0.19 | 0.023 | 0.005 | 0.003 |
| Cranium | 1.85 | 1.09E−01 | 4.72 | 14.43 | 4.19 | 44.60 | – | 0.22 | 10.49 | 0.31 | – | – | 20.99 | – | 0.01 |
| Tumor, brain parenchyma | 1.03 | 1.04E−01 | 11.06 | 12.54 | 1.33 | 73.77 | 0.18 | 0.01 | 0.35 | 0.17 | 0.23 | 0.31 | 0.01 | 0.01 | 0.001 |
*A. Density: total atom density.
The change of weighting and energy for proton beams can be obtained from the flux passing through the range modulation wheel in the nozzle of the treatment machine and the range-compensated range, but can also be calculated mathematically (26-28). In this study, the energy spectrum of the proton’s spread-out Bragg peak (SOBP) was calculated by applying the mathematical method proposed by Jette and Chen (29) and Bortfeld (30). Protons were injected perpendicular to the surface of the phantom onto a field of size 10×10 cm2. For the physical model, QGSP_BIC, which includes a standard electromagnetic model, was applied. The lower limit of the particle tracking range was set at 1 mm, and Auger electrons generated from the de-excitation process in the material were included in the computer simulation. The initial particle transport was set at 5×108 source particle histories, considering the statistical error. To simulate the dose enhancement in the tumor volume, Au and Gd were applied at concentrations of 10, 20, and 30 mg/g based on previous results (16,19,31). For the interactions caused by the enhancement phenomenon in the phantom, the change ratio of the reaction caused by the interaction of the initial particles with the material were calculated according to the quality of radiation, enhancement material, and concentration using Geant4’s sensitive detector. Secondary particles produced through this process were subsequently tracked and simulated to obtain the particle fluence and energy absorbed by deposition.
In addition to the fluence of secondary particles, the absorbed dose by Geant4’s sensitive detector is calculated as the equivalent dose considering the weight of the beam quality. The equivalent dose calculated from radiation weighting factor (WR) in publications 103 and 119 of the International Commission on Radiological Protection (32,33) can be expressed as Eq. [1]: Geant4’s sensitive detector. Secondary particles produced through this process were subsequently tracked and simulated to obtain the particle fluence and energy absorbed by deposition.
where HT is the equivalent dose in Sieverts (Sv) by tissue T, WR is the radiation weighting factor, DR is the absorbed in grays (Gy) by radiation type R. Similarly, the frequency of physical processes and the generation of secondary particle from the dose enhancement material was also analyzed.
Results
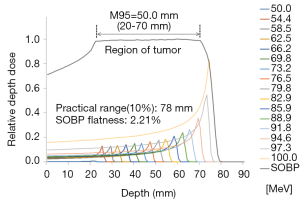
To adequately contain the tumor tissue, the SOBP in the water phantom was represented using the mathematical method proposed by Bortfeld (30). The constituent energy was divided into 16 levels ranging from 50–100 MeV. The energy and relative weight for each interval are listed in Table 2. The 95% modulation range (M95) was 2–7 cm, the interval length was 5 cm, the practical range for 100% dose was 7.8 cm, and the flatness was 2.21% (Figure 2).
Table 2
| No. | ek* | wk# |
|---|---|---|
| 1 | 50.00 | 0.0016 |
| 2 | 54.39 | 0.0241 |
| 3 | 58.53 | 0.0258 |
| 4 | 62.45 | 0.0276 |
| 5 | 66.19 | 0.0297 |
| 6 | 69.77 | 0.0321 |
| 7 | 73.22 | 0.0349 |
| 8 | 76.54 | 0.0381 |
| 9 | 79.76 | 0.0420 |
| 10 | 82.88 | 0.0468 |
| 11 | 85.92 | 0.0529 |
| 12 | 88.87 | 0.0613 |
| 13 | 91.75 | 0.0737 |
| 14 | 94.56 | 0.0960 |
| 15 | 97.31 | 0.1507 |
| 16 | 100.00 | 0.2459 |
*, corresponding energy for the k interval (MeV); #, normalized beam weights.
The frequency of interactions in tumor tissue without dose enhancement material is outlined in Table 3. The frequency of interaction was 99.02% for inelastic Coulomb scattering, which is caused by electrical interaction with electrons, and other interaction processes showed very low frequencies (0.633% for elastic collision, 0.334% for nuclear inelastic collision, and less than 0.006% for multiple Coulomb scattering; see Table 3). The use of Au as the enhancement material increased the frequency of interactions by a factor of 1.14–1.18 for inelastic Coulomb scattering, 1.05–1.30 for elastic collision, 1.03–1.37 for nuclear inelastic collision, and 1.12–1.55 for multiple Coulomb scattering. The use of Gd as the enhancement material increased the frequency of interactions by a factor of 1.08–1.14 for inelastic Coulomb scattering, 1.03–1.25 for elastic collision, 1.01–1.34 for nuclear inelastic collision, and 1.11–1.45 for multiple Coulomb scattering (Figure 3). The dose enhancement caused greater changes in the frequency of interactions as the concentration of the enhancement material increased. Also, the nuclear inelastic collision and elastic collision increased more than the inelastic Coulomb scattering. The production of secondary particles caused by the interaction with protons can be quantified by the physical action of energy loss through nuclear inelastic collisions in the material, and the production of secondary particles was confirmed in the (p, α), (p, n), (p, γ), and (p, d) reactions. The particle fluence per incident proton was 2.12E−03 cm−2 for alpha particles, 1.17E-03 cm−2 for neutrons, 1.73E−03 cm−2 for gamma rays, and 5.23E−04 cm−2 for deuterons without dose enhancement material (Figure 4). Consequently, the equivalent dose in the absence of dose enhancement material was 4.378E+01 pSv for alpha particles, 4.351E−03 pSv for neutrons, 4.599E−07 pSv for gamma rays, and 2.377E+01 pSv for deuterons (Table 4). The increased frequency of nuclear inelastic collision caused by the interaction with the dose enhancement material led to the production of secondary particles and an increase in the equivalent dose. The use of Au as the enhancement material increased the equivalent dose by a factor of 1.032–1.070 for alpha particles, 1.133–1.860 for neutrons, 1.030–1.053 for deuterons, and 37.03–384.68 for gamma rays. The use of Gd as the enhancement material increased the equivalent dose by a factor of 1.015–1.043 for alpha particles, 1.075–1.478 for neutrons, 1.021–1.036 for deuterons, and 25.64–252.70 for gamma rays (Figure 5). The change in dose from the secondary particle production caused by the nuclear inelastic collision reaction rose as the concentration of the enhancement material increased, and the use of Au as the enhancement material caused a greater change in dose than Gd. Furthermore, gamma rays produced the greatest change in the equivalent dose from the secondary particles, followed by neutrons, alpha particles, and deuterons.
Table 3
| Variable | Interaction process | |||
|---|---|---|---|---|
| Inelastic Coulomb scattering | Elastic collision | Inelastic collision | MCS* | |
| Frequency (%) | 99.02 | 0.633 | 0.334 | 0.006 |
*, multiple Coulomb scattering.

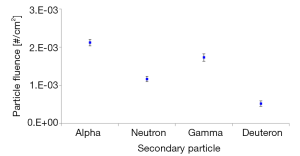
Table 4
| Variable | Secondary particle | |||
|---|---|---|---|---|
| Alpha | Neutron | Gamma | Deuteron | |
| HT* | 4.378E+01 | 4.351E−03 | 4.599E−07 | 2.377E+01 |
*, equivalent dose, unit: pSv.

Discussion
Polf et al. (34) conducted dose enhancement using protons with Au particles in prostate cancer cells, and reported that the dose enhancement factor increased by 10–15%, whereas Kim et al. (35) reported a high-volume reduction in tumor tissue with Au particles and protons at 45 MeV. Thus, some researchers have reported the effects of dose enhancement using protons, but studies on the generation of electrons from ionization and the mechanism of physical reactions with these electrons are limited. This study has calculated the proton spectra of SOBP and analyzed physical interactions of enhancement materials such as Au and Gd, and evaluated the changes in the production of secondary particles.
It has been found that the physical actions of protons in a material mostly consist of ionization by the Coulomb force, and the frequency of energy loss by nuclear inelastic collision is very low (36). To analyze the changes in the frequency of interactions under various enhancement materials, the interactions inside the tumor tissue were traced from the initial particles using Monte Carlo simulations. Inelastic Coulomb scattering by the Coulomb force occurred in over 90% of interactions, with elastic collision, nuclear inelastic collision, and multiple Coulomb scattering appearing at low frequencies. Also, the higher the concentration of dose enhancement material was increased the frequency of interactions. This phenomenon appears to be due to the increase in ionization caused by the enhanced mass-stopping power of the enhancement material. An increased frequency of interactions in a material can decrease the protons’ range and SOBP range. Ahmad et al. (37) reported 30–38% reduction of range in the interactions between 60 MeV proton and high atomic number material such as aurum and platinum, higher the atomic number of the material was reduced range of Bragg peaks.
The production of secondary particles was analyzed for the alpha particles, neutrons, deuterons, and gamma rays. Increased production of secondary particles from interaction of dose enhancement material, such as Au and Gd. Specifically, the equivalent dose increased by factors of up to 1.86 and 384.68 with neutrons and gamma rays, respectively. Dawidowska et al. (38) reported production of 0.1%, 0.4%, 0.5%, 0.6%, and 0.7% of neutrons from protons with energies of 50, 55, 60, 65, and 70 MeV, suggesting that higher incident energy in the protons increases neutron production. Based on this result, the production of secondary particles will increase further before the protons reach the tumor tissue inside the simulated body. According to Mowlavi et al. (39), the frequency of interactions in materials with 30–60 MeV protons was greater than 99% for the ionization process, and lower than 1% for nuclear inelastic collision. This is similar to the results found in this study, which showed a frequency of 0.7% for nuclear inelastic collision. Thus, it is estimated that the transmitted dose of secondary particles generated from nuclear inelastic collisions, which occur at a very low frequency in the interaction between protons and the enhancement material, will be very small. However, as the dose realized by secondary particles produced in a material cannot be removed and has a significant biological effect, this phenomenon may increase the possibility of probabilistic disorders such as secondary cancer. Therefore, it is very important to identify these physical properties.
Conclusions
The physical characteristics of the dose enhancement phenomenon and secondary particle production were evaluated with the SOBP. More than 99% of the physical interactions of the SOBP were found to consist of energy transmission by inelastic Coulomb scattering due to electrical actions. In the dose enhancement process, the frequency of physical interactions was increased by dose enhancement material, such as Au and Gd. The production of secondary particles from nuclear inelastic collisions confirmed that, as the concentration of the enhancement material increases, the equivalent dose also increases. The dose increased by factors of up to 1.86 and 384.68 with neutrons and gamma rays, respectively. The dose enhancement simulations conducted in this study correspond to the physical characteristics of energy transmission, and the results of this study are expected to be used as basic data for in vivo and in vitro experiments investigating the effects of dose enhancement.
Acknowledgments
Funding: This work was supported by
Footnote
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tcr.2019.07.54). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Pollack A, Zagars GK, Starkschall G, et al. Prostate cancer radiation dose-response: results of the M.D. Anderson Phase III randomized trial. Int J Radiat Oncol Biol Phys 2002;53:1097-105. [Crossref] [PubMed]
- Bednarz B, Daartz J, Paganetti H. Dosimetric accuracy of planning and delivering small proton therapy fields. Phys Med Biol 2010;55:7425-38. [Crossref] [PubMed]
- Besemer A, Paganetti H, Bednarz B. The clinical impact of uncertainties in the mean excitation energy of human tissues during proton therapy. Phys Med Biol 2013;58:887-902. [Crossref] [PubMed]
- Cho J, Ibbott G, Gillin M, et al. Determination of elemental tissue composition following proton treatment using positron emission tomography. Phys Med Biol 2013;58:3815-35. [Crossref] [PubMed]
- Lyman JT. Complication probability as assessment from dose-volume histograms Radiat Res 1985;104:13-9. [Crossref]
- Stavrev P, Stavreva N, Niemierko A. Generalization of a model of tissue response to radiation based on the ideas of functional subunits and binomial statistics. Phys Med Biol 2001;46:1501-18. [Crossref] [PubMed]
- Shiu A, Mellenberg D. General practice of radiation oncology physics in the 21st century. Medical Physics Publishing, 2000.
- Regulla D, Schmid E, Friedland W, et al. Enhanced values of the RBE and H ratio for cytogenetic effects induced by secondary electrons from an X-irradiated gold surface. Radiat Res 2002;158:505-15. [Crossref] [PubMed]
- Sardi JE, Boixadera MA, Sardi JJ. A critical overview of concurrent chemoradiotherapy in cervical cancer. Curr Oncol Rep 2004;6:463-70. [Crossref] [PubMed]
- Sim L, Fielding A, English M, et al. Enhancement of biological effectiveness of radiotherapy treatments of prostate cancer cells in vitro using gold nanoparticles. Coogee Beach, Sydney, International Nanomedicine Conference, 2011.
- Kok HP, Crezee J, Franken NA, et al. Quantifying the combined effect of radiation therapy and hyperthermia in terms of equivalent dose distributions. Int J Radiat Oncol Biol Phys 2014;88:739-45. [Crossref] [PubMed]
- Brun E, Sanche L, Sicard-Roselli C. Parameters governing gold nanoparticle X-ray radiosensitization of DNA in solution. Colloids Surf B Biointerfaces 2009;72:128-34. [Crossref] [PubMed]
- Berbeco R, Korideck H, Ngwa W, et al. TU-C-BRB-11: In vitro dose enhancement from gold nanoparticles under different clinical MV photon beam configurations. Med Phys 2012;396:3900. [Crossref]
- Khan FM, Gibbons JP. The physics of radiation therapy, Fourth edition. Wolters Kluwer Lippincott Williams & Wilkins 2015:524-53.
- Pérez-López CE, Garnica-Garza HM. Monte Carlo modeling and optimization of contrast-enhanced radiotherapy of brain tumour. Phys Med Biol 2011;56:4059-72. [Crossref] [PubMed]
- Zhang DG, Feygelman V, Moros EG, et al. Monte Carlo study of Radiation Dose Enhancement by Gadolinium in Megavoltage and High Dose Rate Radiotherapy. PLoS One 2014;9:e109389. [Crossref] [PubMed]
- Unezaki S, Maruyama K, Hosoda JI, et al. Direct measurement of the extravasation of polyethyleneglycol coated liposomes into solid tumour tissue by in vivo fluorescence microscopy. Int J Pharm 1996;144:11-7. [Crossref]
- Greish K. Enhanced permeability and retention (EPR) effect for anticancer nanomedicine drug targeting. Methods Mol Biol 2010;624:25-37. [Crossref] [PubMed]
- Mesbahi A, Jamali F, Gharehaghaji N. Effect of photon beam energy, gold nanoparticle size and concentration on the dose enhancement in radiation therapy. BioImpacts 2013;3:29-35. [PubMed]
- Delaram P, Mahdi G, Mehdi M. Tumor dose enhancement by gold nanoparticles in a 6 MV photon beam: a Monte Carlo study on the size effect of nanoparticles. Nukleonika 2013;58:275-80.
- Kim SR. Feasibility study on the use of gold nanoparticles as a dose enhancement agent for a superficial X-ray therapy applied to melanoma. Seoul National University Graduate School, 2014.
- Khoei S, Mahdavi SR, Fakhimikabir H, et al. The role of iron oxide nanoparticles in the radiosensitization of human prostate carcinoma cell line DU145 at megavoltage radiation energies. Int J Radiat Biol 2014;90:351-6. [Crossref] [PubMed]
- Choi E, Son J. Biophysical evaluation of radiosensitization by AuNPs nanoparticles irradiated photon beam. J Korean Soc Radiol 2016;10:483-7. [Crossref]
- Echkerman KF, Cristy M, Ryman JC. The ORNL mathematical phantom series. 1996. Available online: http://homer.ornal.gov/vlab/mird2.pdf
- ICRU. Photon, electron, proton and neutron interaction data for body tissues. ICRU Report 46. International Committee on Radiation Units and Measurements, Bethesda, MD, 1992.
- Kooy HM, Schaefer M, Rosenthal S, et al. Monitor unit calculations for range-modulated spread-out Bragg peak fields. Phys Med Biol 2003;48:2797-808. [Crossref] [PubMed]
- Kooy HM, Rosenthal SJ, Engelsman M, et al. The prediction of output factors for spread-out proton Bragg peak fields in clinical practice. Phys Med Biol 2005;50:5847-56. [Crossref] [PubMed]
- Kang JH, Wilkens JJ, Oelfke U. Demonstration of scan path optimization in proton therapy. Med Phys 2007;34:3457-64. [Crossref] [PubMed]
- Jette D, Chen W. Creating a spread-out Bragg peak in proton beams. Phys Med Biol 2011;56:N131-8.
- Bortfeld T. An analytical approximation of the Bragg curve for therapeutic proton beam. Med Phys 1997;24:2024-33. [Crossref] [PubMed]
- Chow JC, Leung MK, Jaffray DA. Monte Carlo simulation on a gold nanoparticle irradiated by electron beams. Phys Med Biol 2012;57:3323-31. [Crossref] [PubMed]
- ICRP. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103. Ann ICRP 2007;37:1-332. [PubMed]
- ICRP. ICRP Publication 119: Compendium of dose coefficients based on ICRP Publication 60. Ann ICRP 2012;41:1-130. [Crossref] [PubMed]
- Polf JC, Bronk LF, Driessen WH, et al. Enhanced relative biological effectiveness of proton radiotherapy in tumor cells with internalized gold nanoparticles. Appl Phys Lett 2011;98:193702. [Crossref] [PubMed]
- Kim JK, Seo SJ, Kim HT, et al. Enhanced proton treatment in mouse tumors through proton irradiated nanoradiator effects on metallic nanoparticles. Phys Med Biol 2012;57:8309-23. [Crossref] [PubMed]
- NIST. Stopping-Power & Range Tables for Electrons, Protons, and Helium Ions, 2017.
- Ahmad R, Royle G, Lourenco A, et al. Investigation into the effects of high-Z nano materials in proton therapy. Phys Med Biol 2016;61:4537-50. [Crossref] [PubMed]
- Dawidowska A, Paluch Ferszt M, Konefal A. The determination of a dose deposited in reference medium due to (p,n) reaction occurring during proton therapy. Rep Pract Oncol Radiother 2014;19:S3-8. [Crossref] [PubMed]
- Mowlavi AA, Fornasie MR, de Denaro M. Calculation of energy deposition photon and neutron production in proton therapy of thyroid gland using MCNPX. Appl Radiat Isot 2011;69:122-5. [Crossref] [PubMed]