
Benchmarking of electron beam parameters based on Monte Carlo linear accelerator simulation
Introduction
Monte Carlo simulation of coupled photon-electron transport and dose calculations in heterogeneous media is proved as an accurate method in many studies (1-3). With the development of radiotherapy, Monte Carlo codes have been successfully implemented in the treatment planning system (TPS) to calculate dose distributions. The challenging part of applying Monte Carlo algorithms in TPS is to decrease the discrepancies between calculated and measured doses (4). Accurate calculated doses can also be a standard to verify the measured doses in some situations such as the unexpected problems occurring in the accelerators and detectors. The issues mentioned both need precise dose distributions which can be achieved by an accurate Monte Carlo model. And the incident electron beam parameters are essential in the model. Because they were shown to have obvious impacts on the depth doses and lateral dose profiles in several studies (5-8), the electron energy, the radial intensity distribution (given by σ, the standard deviation in the Gaussian distribution) and the mean angular spread of the electron beams have to be determined.
Many studies proposed some methods to determine the parameters by matching the measured and calculated doses in various fields. However, to get satisfying agreements, a lot of work needs to be done. When the concern is on some certain size fields, it is more efficient to benchmark the parameters based on the dose characteristics in the fields. This study is to propose a benchmarking procedure and figure out how the parameters affect the dose distributions for a frequently-used 10×10 cm2 field.
In general, it is influenced by two or three incident electron beam parameters in dose distribution. The method that the electron energy determined by matching the depth doses is required to meet the following two conditions: (I) local dose difference (percentage difference between calculated and measured doses) is below 1% when the σ is changed in certain range. The influence of radial intensity on the depth doses is negligible; (II) mean angular spread has little effect on the percentage depth doses (9).
In determination of electron radial intensity, it is necessary to exclude the electron energy influence on the lateral dose profiles. And we found that the calculated lateral dose profiles had nearly no difference compared to measured doses, when the electron energy varied from 5.5 to 6.4 MeV. In this study, penumbra doses are used to determine the radial intensity rather than main field doses. Because there is no significant dose difference in the main field but clear dose discrepancies in penumbra region when the σ is in the 0.0–1.9 cm range.
We propose the conditions under which the electron energy and radial intensity can be determined by matching depth doses and lateral doses respectively. In the process of independent determination of electron energy and radial intensity, the linear regression and penumbra matching were adopted to find the optimal values. The optimal electron energy and radial intensity are suggested to find in 5.5–6.4 MeV and 0.05–0.15 cm respectively. The mean angular spread was tuned to get better matching of lateral doses at different depths.
Methods
Equipment and device
The Monte Carlo users code EGSnrc (10,11) is used to simulate the radiation transport in the accelerator treatment head and dose deposition in the phantom for a VARIAN IX linear accelerator operating at 6 MV. The subroutine BEAMnrc (12) produces phase space file (PHSP) (13,14) which contains the particles information after crossing the treatment head. Then the particles in the file were taken as the subroutine DOSXYZnrc (15) input source to calculate dose distributions in the phantom. Depth doses and dose profiles were measured in a water phantom with an ionization chamber (Semiflex, PTW SCANLIFT). Source surface distance was 100 cm both in simulation and measurement.
BEAMnrc accelerator Monte Carlo model
The dimensions and materials of components in the model were provided by the vendors. The modules of target, primary collimator, vacuum window, flatten filter, ionization chamber, field mirror, secondary collimator (Jaws) in the treatment head were modeled by SLABS, CONS3R, SLABS, FLATFILT (16), CHAMBER, MIRROR, JAWS correspondingly in the BEAMnrc routine. Phase space files were scored at a plane which was perpendicular to the Z axis (beam direction) with 100 cm source surface distance. Variance reduction technique was Directional Bremsstrahlung Splitting (17). ECUT (global cutoff energy for electron transport, total energy will deposit in the current region when it falls below the value) was set to 0.70 MeV. PCUT (global cutoff energy for photon transport, the meaning is equivalent of ECUT) was 0.01 MeV.
The incident electron beams have a Gaussian distribution in X and Y direction (source number 19 in BEAMnrc). The monoenergetic beams were adopted, instead of those with spectrum, because the differences between the two dose distributions caused by this factor are very tiny. The circular electron beam was used both in depth dose and dose profile simulations. A σ value of 0.1 cm was used in the depth dose simulation while the σ varied between 0.0–0.2 cm was used in dose profile simulation. The mean angular spread was always set to 0° before the energy and radial intensity were determined and changed between 0°–0.7° to match the lateral dose profiles.
Dose calculation in DOSXYZnrc
The phase space files were as the input files (source number 2 in DOSXYZnrc) to calculate depth and lateral dose distributions in the phantom which is in Cartesian coordinate. The phantom was defined as the following directions: X axis is in the in-plane direction; Y axis is in the cross-plane direction; Z axis (central axis, CAX) is in the beam direction. The origin of the three-dimensional coordinate is in the center of plane at the top of the phantom which is coincided with the phase space files. To reduce simulation time and keep the resolution in the interested region, the phantom was divided into different voxel sizes. ECUT and PCUT were same as the values in BEAMnrc. Electron step algorithm and boundary crossing algorithm were PRESTA-II and EXACT.
Percentage depth doses were calculated in a 40×40×40 cm3 water phantom. The voxel dimensions around the central axis were 1.0×1.0 cm2 at the X-Y plane, while the size in the Z direction was set according to the measurements. The statistical uncertainties of the depth doses were equal or less than 1% of local dose value for voxels at depths between 0.4–28 cm.
Dose profiles were taken into consideration only in the in-plane direction because of the symmetry of accelerator head and circular incident electron beam. The phantom size was the same as the one in the depth dose simulation. Voxel dimensions in the in-plane and cross-plane directions was 0.4 and 1.0 cm respectively, and the dimensions in the beam direction at 1.5, 5, 10, 20, 30 cm depths were 0.4 cm. In the main field area, the statistical uncertainties were all below 1.2%, with an exception for dose profiles at 30 cm depth of which it was below 1.6%.
Depth doses and lateral dose profiles measurement
The depth doses and dose profiles were measured with an ionization chamber (Semiflex 31010), because it has potential quality to get accurate dose distributions for photon beams (18,19). The chamber is driven by an electrical machine controlled by the scanning system (MEPHYSTO-mc2) in a water phantom (MP3). The resolution and positional accuracy of the phantom are both 0.1 mm. The active volume and cavity diameter of the chamber are 0.125 cm3 and 5.5 mm respectively.
Results
Depth doses
Calculated and measured depth doses were both normalized to the maximum dose at 1.5 cm depth. The percentage depth doses were mostly within 0.8% of measurements at the considered depths when the electron energy was set to 5.95 MeV as shown in Figure 1A. In order to distinguish the ideal energy value with an accuracy of 0.05 MeV, the local dose differences between calculated and measured depth dose distributions were dealt with least-square linear regression. A better matching could be indicated by a line with zero slope and minor intercept. Dose differences were demonstrated in Figure 1B,C,D for three energies and the results showed that 5.95 MeV was the optimal energy. The linear regressions for rest electron energies starting from 5.4 to 6.5 MeV with the increment of 0.1 MeV are depicted as Table 1. Figure 2 shows the negligible dose differences when the radial intensity was varied from 0.1 to 0.4 cm with the same energy equal to 5.95 MeV.

Table 1
| Energy/MeV | Least-square linear regression |
|---|---|
| 5.4 | y=–0.060x+0.434 |
| 5.5 | y=–0.057x+0.693 |
| 5.6 | y=–0.042x+0.582 |
| 5.7 | y=–0.017x–0.052 |
| 5.8 | y=0.0097x–0.849 |
| 6.1 | y=–0.04x+1.628 |
| 6.2 | y=0.022x–0.223 |
| 6.3 | y=0.209x+0.167 |
| 6.4 | y=0.019x+0.139 |
| 6.5 | y=–0.003X+1.149 |
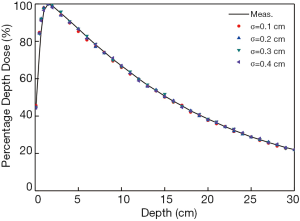
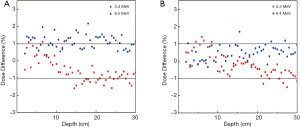
The electron energy had insignificant impacts on the depth doses when it fluctuated around the nominal energy. However, when the energy was beyond the certain range, the dose differences were obvious. Therefore, it is necessary to figure out the range to provide a reference for energy determination. Dose differences for different electron energies are included in Figure 3. The dose differences are mostly below 1% in Figure 3B which indicate a more reliable dose distribution. Hence, the proper energy range is suggested from 5.5 to 6.4 MeV.
Lateral dose profiles
Electron energy
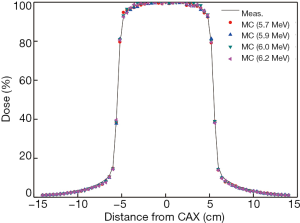
The dose profiles at 10 cm depth calculated with different electron energies are shown in Figure 4. All calculated and measured doses were normalized to the dose in a voxel at the center of X axis. There were no apparent differences among the curves produced by 4 different energies. Calculated doses in the main field and penumbra region also had a good fit with the measured dose profiles.
Radial intensity distribution
The local dose differences in the main field were lower than 1.4% for various σ values as shown in Figure 5A. When the radial intensity was increased to 0.20 cm, large discrepancies in the field began to emerge as revealed in Figure 5B. On account of no significant dose differences in the main field for a radial intensity below 0.20 cm, a new way was used for the radial intensity determination by matching calculated and measured doses in the penumbra region. It was shown that the local dose difference got its minimum value of 0.15% when the radial intensity was 0.10 cm in Table 2. The deviation is larger when the radial intensity is less than 0.05 cm or greater than 0.15 cm.
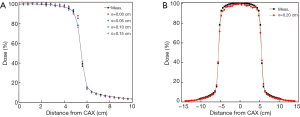
Table 2
| Radial intensity/cm | 0.0 | 0.03 | 0.05 | 0.08 | 0.10 | 0.13 | 0.15 | 0.18 | 0.20 |
|---|---|---|---|---|---|---|---|---|---|
| Dose difference/% | 9.84 | 7.85 | 7.35 | 3.26 | 0.15 | 2.01 | 3.45 | 4.18 | 8.03 |
Mean angular spread
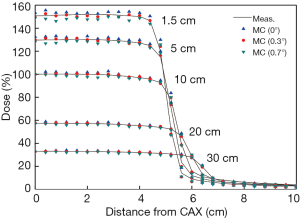
In this section, the electron energy was set to 5.95 MeV, and the radial intensity was 0.10 cm. Calculated and measured dose profiles at all depths were normalized to the same dose point which was at the 10 cm depth in the central axis. Figure 6 indicated that good agreements between measurement and calculation within the main field area and penumbra region were gained at five different depths by introducing a 0.3° mean angular spread. Doses calculated with smaller mean angular spread were higher than measured dosed both in main field and penumbra region at all depths.
Discussion
Determining the optimal electron beam parameters is an important step to guarantee the accuracy of Monte Carlo simulation photon doses. These parameters are not explicitly known but have major influence on the dose distributions (20). Based on our research, the following benchmarking procedure is proposed: Firstly, the energy is determined by matching calculated and measured depth dose and kept the same value in the next steps; Secondly, the radial intensity is determined by matching the calculated and measured cross field profiles in the penumbra regions. Lastly, the mean angular spread is tuned to decrease the deviation trend of calculated and measured lateral dose profiles at different depths.
Concerning the effect of electron energy on the depth doses, Tzedakis et al. (21) concluded that the maximum absolute value of local dose difference for 5, 6, 7 MeV energy was 1.7%, 0.8%, 1.8% respectively. Chibani et al. (22) found that it had no effect on depth doses when the energy changed around the energy provided by the vendor at a 0.20 MeV interval. In another application, Tai et al. (23) determined the electron energy and radial intensity distribution for Siemens Primus linear accelerator. They found that a good match between measurement and simulation of electron energy was achieved by importing a 6.04 MeV energy value in a 10×10 cm2 field. In the present study, calculated doses of 5.4, 6.5 and 5.5 MeV, 6.4 MeV were compared with measured doses to find a range where the energy had no impacts on depth doses. An energy range between 5.5 to 6.4 MeV was suggested to the same type accelerator. The energy value of 5.95 MeV was used in the simulation where the radial intensity was changed from 0.10 to 0.40 cm. The results indicated that there was no influence on the depth doses when the radial intensity was changed in this range. Based on the results, the electron energy can be determined by matching depth dose individually as shown in Table 3.
Table 3
| Electron beam parameter | Effect on | |
|---|---|---|
| Depth dose | Lateral dose profile | |
| Energy | Yesa | No |
| Radial intensity (σ) | No | Yesb |
| Mean angular spread | No | Yesc |
a, energy out of 5.5–6.4 MeV range results non-ignorable depth dose differences; b, radial intensity of σ value in the range 0.0–0.19 cm has negligible effects on the dose profiles in the main field but a notable difference with measured dose in the penumbra areas; c, 0.3° mean angular spread results an acceptable agreement for dose profiles at different depths.
The electron beam radial intensity distribution has a significant impact on the lateral dose profiles. Sheikh-Bagheri and Rogers (5) compared the off-axis factors produced by different radial intensity from 0.01 to 0.19 cm with measured off-axis factors. With a smaller or larger σ (such as a value closed to 0 or 0.19 cm) involved, off-axis factors had obvious differences compared with the ones calculated with a 0.1 cm value, especially in the points far away from central axis. The finding indicates that the radial intensity distribution has effects on the doses out of main field which is the same as the result in our study. In Chibani et al.’s study (22), no difference was found in the main field region between calculated and measured dose profiles when σ were 0.04 cm and 0.12 cm. As the σ changed from 0.0 to 0.19 cm in our research, good match was also found in the main field region.
The penumbra area is the sum of geometric, penetrating and scattering penumbras. In other words, doses in the penumbra region are influenced by the size of the source (24,25), the penetrating doses from the collimators (26) and the scattering doses in the phantom. In this study, we only consider the influence of the geometric penumbra, as the other two penumbras are considered to remain unchanged. Discrepancies in the penumbra area can be explained that the radial intensity has some effects on the shape of source which can affect the penumbra doses. Since electron energy has no influence on the size of source, penumbra match has the advantage that the radial intensity distribution can be determined by little influence of any inaccuracies in electron energy.
The mean angular spread is a tiny angle between Z axis and incident beam direction specified at half-width at half maximum of the electron radial intensity distribution. Thus, it makes a difference on the dose profiles. The bremsstrahlung photons emitted by the electron beams with larger radial intensity are blocked more efficiently by the primary collimator, reducing the amount of scattering doses, which can explain the trend when the mean angular spread was increased. With an 0.3° mean angular spread involved, the dose profiles had good agreements with measured doses at all interested depths.
Conclusions
Benchmarking a Monte Carlo model which contains the physical accelerator model and incident electron beam model is a time-consuming task. In view of the important influences of electron beam parameters on the dose distributions, simplified procedure is proposed to determine electron beam parameters according to the data in the present and previous studies for a 10×10 cm2 field. The procedure will be used in other size fields to determine the beam parameters in our next research. The main conclusions are included as the following:
- Electron energy and radial intensity distribution can be determined independently based on the results concluded from a 10×10 cm2 field;
- Radial intensity is determined by matching the calculated and measured doses in the penumbra region rather than in the main field;
- It is feasible to tune the mean angular spread to get better match between calculated and measured dose profiles at different depths;
- The ideal electron energy and radial intensity value are suggested to find in 5.5-6.4 MeV and 0.05-0.15 cm respectively. With 5.95 MeV mean energy, 0.10 cm radial intensity and 0.3° mean angular spread involved, accurate percentage depth doses and lateral dose profiles are achieved.
Acknowledgments
Funding: The study was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tcr.2019.12.02). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was approved by Institutional Research Human or Animal Ethics Committee of Qingdao Municipal Hospital and the ID/number is 2019043.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Rogers DWO, Bielajew AF. Monte Carlo techniques of electron and photon transport for radiation dosimetry. The dosimetry of ionizing radiation 1990;3:427-539.
- Andreo P. Monte Carlo techniques in medical radiation physics. Phys Med & Biol 1991;36:861-920. [Crossref] [PubMed]
- DeMarco JJ, Solberg TD, Smathers JBA. CT-based Monte Carlo simulation tool for dosimetry planning and analysis. Med Phys 1998;25:1-11. [Crossref] [PubMed]
- Chetty IJ, Curran B, Cygler J E, et al. Report of the AAPM Task Group No. 105: Issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning. Med Phys 2007;34:4818-53. [Crossref] [PubMed]
- Sheikh-Bagheri D, Rogers DWO. Sensitivity of megavoltage photon beam Monte Carlo simulations to electron beam and other parameters. Med Phys 2002;29:379-90. [Crossref] [PubMed]
- Pena J, Gonzalez-Castano DM, et al. Automatic determination of primary electron beam parameters in Monte Carlo simulation. Med Phys 2007;34:1076-84. [Crossref] [PubMed]
- Wang LLW, Leszczynski K. Estimation of the focal spot size and shape for a medical linear accelerator by Monte Carlo simulation. Med Phys 2007;34:485-8. [Crossref] [PubMed]
- Sham E, Seuntjens J, Devic S, et al. Influence of focal spot on characteristics of very small diameter radiosurgical beams. Med Phys 2008;35:3317-30. [Crossref] [PubMed]
- Almberg SS, Frengen J, Kylling A, et al. Monte Carlo linear accelerator simulation of megavoltage photon beams: Independent determination of initial beam parameters. Med Phys 2012;39:40-7. [Crossref] [PubMed]
- Kawrakow I. Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version. Med Phys 2000;27:485-98. [Crossref] [PubMed]
- Kawrakow I. The EGSnrc code system: Monte Carlo simulation of electron and photon transport. NRCC Report 2009 PIRS-701.
- Rogers DWO, Faddegon BA, Ding GX, et al. BEAM: A Monte Carlo code to simulate radiotherapy treatment units. Med Phys 1995;22:503-24. [Crossref] [PubMed]
- Martins JC, Saxena R, Neppl S, et al. Optimization of phase space files from clinical linear accelerators. Phys Medica 2019;64:54-68. [Crossref] [PubMed]
- Teke T, Duzenli C, Bergman A, et al. Monte Carlo validation of the TrueBeam 10XFFF phase-space files for applications in lung SABR. Med Phys 2015;42:6863-74. [Crossref] [PubMed]
- Walters BRB, Rogers DWO. DOSXYZnrc Users Manual, NRCC Report PIRS-794. Ottawa (ON): National Research Council of Canada, 2002.
- Almberg SS, Frengen J, Lindmo T. Monte Carlo study of in-field and out-of-field dose distributions from a linear accelerator operating with and without a flattening-filter. Med Phys 2012;39:5194-203. [Crossref] [PubMed]
- Kawrakow I, Rogers DWO, Walters B. Large efficiency improvements in BEAMnrc using directional bremsstrahlung splitting. Med Phys 2004;31:2883-98. [Crossref] [PubMed]
- Andreo P, Burns DT, Hohlfeld K, et al. Absorbed dose determination in external beam radiotherapy: An international code of practice for dosimetry based on standards of absorbed dose to water. Iaea Trs, 2000, 398.
- Cao Y, Yang XY, Yang Z. Superficial dose evaluation of four dose calculation algorithms. Radiat Radia Phys Chem 2017;137:23-8. [Crossref]
- Horova S, Judas L. Monte Carlo modelling of clinical accelerator beams and estimation of primary electron beam parameters. Radioprotection 2018;53:61-6. [Crossref]
- Tzedakis A, Damilakis JE, Mazonakis M, et al. Influence of initial electron beam parameters on Monte Carlo calculated absorbed dose distributions for radiotherapy photon beams. Med Phys 2004;31:907-13. [Crossref] [PubMed]
- Chibani O, Moftah B, Ma CMC. On Monte Carlo modeling of megavoltage photon beams: A revisited study on the sensitivity of beam parameters. Med Phys 2011;38:188-201. [Crossref] [PubMed]
- Tai DT, Son ND, Loan TTH, et al. A method for determination of parameters of the initial electron beam hitting the target in linac. J Phys: Conf Ser 2017;851:012032. [Crossref]
- Rodriguez M, Sempau J, Fogliata A, et al. A geometrical model for the Monte Carlo simulation of the TrueBeam linac. Phys Med Biol 2015;60:N219-29.
- Ishizawa Y, Dobashi S, Kadoya N, et al. A photon source model based on particle transport in a parameterized accelerator structure for Monte Carlo dose calculations. Med Phys 2018;45:2937-46. [Crossref] [PubMed]
- Fogliata A, Stravato A, Reggiori G, et al. Collimator scatter factor: Monte Carlo and in-air measurements approaches. Radiat Oncol 2018;13:126. [Crossref] [PubMed]


