Beyond the linear quadratic model: intraoperative radiotherapy and normal tissue tolerance

In clinical practice of radiotherapy it is desirable to use models to estimate the complication risk. Care should be taken when applying models, especially when the clinical dose/volume parameters are beyond the range of data used to generate the model/parameters. Models and dose/volume recommendations are only as good as the data available.

Linear-quadratic model (L-Q model) of radiation effect was originally developed from consideration of subcellular bio-physical events (1,2). In practice, the model has claimed to provide a satisfactory and practical use for explanation of dose/fractionation and biological effect. This model has been applied to both tumor as well as normal tissue. In biological effects of radiation to normal tissue there are different types of radiation damage to cells (i.e., single strand break-SSB, double strand break-double standard break (DSB), and other DNA lesions), different repair mechanism of cells vs. tissues and there are different kinds of cell deaths: reproductive (mitotic), apoptotic and G1 arrest. The L-Q model is developed to use some of the above events (with numerous assumptions) to predict normal tissue radio sensitivity. It is assumed that the frequency of chromosomal aberrations is a L-Q function of dose because the aberrations are consequences of the interaction of two separate DNA breaks. At low doses, both breaks may be caused by the same electron (same ionization event); the probability of exchange aberration is proportional to the dose (D). At the higher doses the two breaks are more likely to be caused by separate electrons, the probably of exchange aberration is proportional to the square of the dose (D²). From the above, the α/β ratio is driven which is a dose in which a single and multi-target mechanisms contribute equally to cell killing in vitro. α/β ratio is a single dose in a continuum of possible doses associated with what is perceived as discontinuous dose response. Doses smaller than D=α/β are presumably associated with the damage small enough to elicit no or little repair, and requiring no extensive time period for any necessary cellular repair; thus, response to such doses (continuum of doses “A” for A_0-i <α/β) is considered to be less sensitive to fractionation. On the other hand, doses exceeding the D=α/β (continuum of doses “B” as B_j-∞>α/β) are considered to be associated with multiple cellular damage and an exponential (quadratic) relation between the dose and the need for cellular repair, leading to an increased responsiveness to fractionation (with fractionation effectively increasing the time for repair and improving resilience). This model heavily depends on cellular capacity for repair; from this we conclude that if α/β ratio is high there is less potential for repair; therefore, a tissue (or tumor) is less sensitive to fractionation. If α/β ratio is low then there is more potential for repair and the tissue is more sensitive to fractionation. Moreover, in theory, for any given dose of B one can anticipate endless permutations for fractionation and dose per fraction leading to the same net effect (same response) on a tissue. This concept underlies iso-effective dose fractionation used in the clinic.

The L-Q model which utilizes α/β ratio is considered to be a quantitative model of cell survival after radiation and it is influenced by the following factors:

• Intrinsic tissue radio-sensitivity;
• Radio-sensitivity in different phases of cell cycle;
• Dose/fractionation;
• Protraction (dose rate);
• Oxygenation;
• Linear energy transfer (LET).

Significant research over the last two decades has been directed to calculate α/β ratio for various early responding and late responding tissues. Table 1 is a select summary of the literature.

Table 1 Normal tissue tolerance-linear quadratic model. What are the α/β-values (GY)?
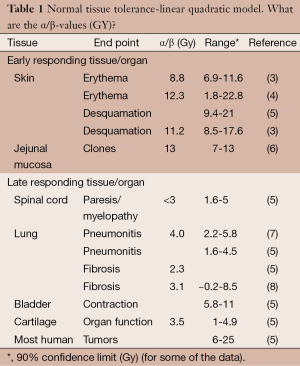
Full table

From the above research we have a series of α/β values for different tissues and even different α/β values for the same tissues; this complicates accurate calculation of iso-effective dose fractionation schedules. At the same time, finding the schedule most damaging to the concrete tumor cells and the least damaging to the surrounding normal tissue is at the core of radiotherapy. Meticulous recording of tissue tolerance for different treatment regimens (for different tissues and different endpoints as complications, e.g., Emami et al. (9) has provided practical estimates of normal tissue tolerance based only on the experience of the authors of the article.

The need in clinical radiotherapy is the means to calculate iso-effective dose fractionation schedule in order to predict normal tissue tolerances probability (NTCP). To achieve this goal, the so-called, “Withers” formula has been used to compare two treatment regimens from which we should be able to calculate what is equivalent dose of a certain dose fractionation to another dose fractionation (10). This formula, based on a L-Q model and utilizing α/β ratio, has gained significant popularity and utility is clinical radiation oncology. However, the following calculation example raises serious concern of the validity of this formula to be routinely utilized in clinical practice.

Test of the validity of biologically iso-effect dose using α/β based formula which is driven by L-Q modeling; model and input for modeling and other assumptions are:

• Organ at risk: spinal cord;
• α/β ratio is reported to be 1.6 to 5 (literature) (we will use values 1, 2, 3 and 4, see Table 2);
  

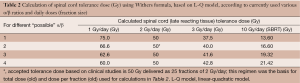  Table 2 Calculation of spinal cord tolerance dose (Gy) using Withers formula, based on L-Q model, according to currently used various α/β ratios and daily doses (fraction size)
  Full table
• Accepted tolerance dose based on clinical studies is 50 Gy/25 F (2 Gy/day);
• Current technology (i.e., IMRT) is capable of any desired dose/volume;
• Withers formula:

  $\mathrm{total}dose(\mathrm{new})=\mathrm{total}dose(\mathrm{old})\times \frac{\alpha /\beta +\mathrm{fraction}size(\mathrm{old})}{\alpha /\beta +\mathrm{fraction}size(\mathrm{new})}$

Clinical interpretation with additional data and conclusion:

• Clinical dose tolerance of spinal cord of 50 Gy/25 Fr (2 Gy/day) is solely based on clinical research regardless of any α/β report with “exotic” doses per fraction;
• No clinician would utilize the above calculated doses (based on α/β) in clinical practice: lack of clinical utility;
• Clinical spinal cord tolerance dose at SBRT is significantly lower than most of the above numbers.

From Withers formula, which is for calculation of iso-effective fraction or total doses a new formula has been driven which is called the biologically effective dose (BED) formula. BED formula is for comparison of different dose fractionation schedules in terms of their biological effectiveness (11).

The formula (when applied to the same tissue, with the same α/β ratio and the same repopulation characteristics) is as follows:

BED=md(GY)×(1+gd(GY)αβ)

The BED is regarded as a measure of true biological dose delivered using a particular combination of dose per fraction d (Gy) and total dose D (Gy) (result of multiplication of d (Gy) and number of fractions) to a given tissue characterized by a specific α/β ratio. G is the factor that considers build-up and decay of radiation damage that occurs with continuous radiation exposure (12). It should be noted that the dose-rate effect does not occur in most situation at dose-rates less than 10 cGy/min due to lower cell killing.

In order to overcome some of the shortcomings of L-Q model in predicting radiation effects in normal tissues or tumors, other models have also been developed. These models include universal survival curve model (13,14), linear-quadratic-linear (LQL) model (or modified L-Q model) (15) and generalized L-Q (g L-Q) model (16). However, none of these models, which are based on some assumptions, have gained widespread clinical utility as will be discussed later. The latest of these newly proposed models suggest to use the L-Q model and incorporate vascular effects of high doses per fraction (17).

Routine acceptance of these L-Q models and use of α/β ratio with numerous (and too liberate) assumptions and shortcomings (more discussed later) in clinical practice on the basis of “in the absence of any other methods for calculating various dose/fractions” is a remarkable tour de force. Nevertheless the rest of this report, which is the review of the literature, will be based on general acceptance of the L-Q model in the literature.

Linear quadratic model (L-Q model): high dose per fraction versus low dose per fraction

Protraction of tumoricidal radiation dose and use of multiple fractions was developed decades ago (long before claim of recent models, and irrespective of L-Q model and α/β ratio), to minimize the damage to normal tissues and therefore to lower the complication rate in day-to-day clinic (18). At that time it was technologically impossible to precisely radiate the target/tumor volume and minimize the amount of surrounding normal tissue to ionizing radiation. Significant technological progress of the last three decades resulted in more precise planning and delivery techniques i.e., 3D CRT, IMRT, IGRT, SRS, and SBRT, etc. Similar progress has also been made in vast utilization of ever progressing diagnostic tools such as CT scan, MRI and PET scan. This has enabled radiation oncologists to accurately and precisely target for radiation the desired, tumor containing, volume of the body and minimize the exposure of normal tissues to ionizing radiation; allowing, in turn, much bolder use of high doses per fraction.

Using high-dose in 1 or few fractions (STS or SBRT) in highly selected patients has resulted in very favorable tumor control and with minimal complication rate. This fractionation which was originally developed for brain tumors, is now in common use for organs outside the brain and with the techniques called SBRT. Now the question is raised as whether the new clinical success is purely a technical progress of applied research with new biology or it can be explained by old biology based on L-Q models. In other words: is this a new wine or is this an attempt to put an old wine in a new bottle. The success of SBRT has now raised a question of whether these large doses per fraction produce greater radiological efficacy than predicted by classic radiobiology or the so-called 5-Rs (19). In classic L-Q model it is assumed that loss of cellular reproductive ability caused by DSBs in DNA is the primary means by which radiation kills cells. Based on the above theory, five factors associated with radiation-cell interactions are considered critical in determining the net effect of radiation therapy on tumors or normal tissues. The so-called 5-Rs include:

• Repair of sublethal cellular damage;
• Repopulation of cells between fractions;
• Redistribution of cells within the cell cycle;
• Re-oxygenation of the surviving cells;
• Radio sensitivity (intrinsic) of cells.

Using L-Q model for calculating biologically iso-effective doses of radiation “requires” only the value of α/β which is usually considered 2-3 for late responding tissues and 10 for acute responding tissues including tumors. As seen in table one, there are significant variations in α/β ratio in various tissues, even a large range of α/β ratios for a given tissue. This places a serious concern in the merit of the so-called α/β ratio in general and specifically when planning SBRT and/or hypofractionation for clinical use, as shown in the previous example (Table 2). In addition to uncertainties of α/β ratio, other factors should also be considered in discussion on validity of any model in high dose per fraction (hypofraction) radiotherapy. The factors include (but are not limited to):

• The cellular α/β ratio in the L-Q model is directly extrapolated from an in vitro survival curve and not accounting for effects on tumor bed which is not applicable to clinical practice;
• L-Q model was initially intended up to dose of up to 6 to 8 Gy per fraction. This model has not been studied for dose per fraction over 10 Gy (11,20,21). Therefore, it cannot empirically extend to higher dose per fraction (as used in SBRT) as suggested by some of the computerized, theoretical calculations (19);
• As has been suggested by Park et al. (22), Song et al. (23) and Sperduto et al. (17), the doses higher than 10 Gy induce vascular damage leading to indirect cell death. The factor has not been taken into consideration in L-Q model;
  • Implicit in modeling of tumor response by the L-Q model is a full re-oxygenation between each dose fraction. This phenomenon has no relation to one single high dose per fraction (STS) (24).;
    • The anti-tumor effect of high radiation dose per fraction such as anti-tumor immunity has not been evaluated (or considered) in L-Q model (25,26).

In conclusion, the validity of L-Q model at high dose per fraction remains controversial and has been investigated by many investigators (13,15-17,19,24,27,28).

Exhaustive review of this subject is beyond the scope of current report, however, overwhelming evidence suggests that L-Q model is inappropriate for high energy, high dose per fraction radiation therapy. As a conceptually flawed model, L-Q can lead to erroneous results when used to calculate iso-effects of radiation. The appropriate modeling of both tumor control and normal tissue toxicities in SRS and SBRT requires application of emerging understanding of molecular, cellular, and tissue level effects of high energy, high dose per fraction ionizing radiation and the role of cancer stem cells.

High energy vs. low energy radiation

Several investigators have developed new miniature X-ray machines for clinical use in radiation therapy operating at low X-ray generating voltages (11,27,29,30). It is now well established that the relative biological effectiveness (RBE) of photons decreases with increasing photon energy (31,32). However, in “classical” radiobiology RBE was associated with a specific tissue type, LET and dose per fraction. Therefore, when a new type of radiation modality was introduced in therapy, it was necessary to determine its RBE relative to the radiation beams already in use and for which the radiation oncologists have accumulated clinical data.

The concept of RBE was initially developed in order to explain the differences in biological effects of ionizing radiations that deposit different amount of energy to the local medium per unit length. The radiation quality is characterized by ionization density in the track given as the LET. The cell survival curves reported for the same absorbed dose delivered by different type of radiation suggest different biological effectiveness for each type of radiation. The major difference between low LET and high LET radiation is in their interactions with the biological systems. Low LET radiation impacts cellular localizations relatively far apart from each other; therefore its effects are spread throughout the cell, delivering a more uniform distribution of ionizations. In contrast, high LET radiation shows well defined, dense tracts of ionization that cause more extensive, albeit localized, damage along the tract. These differences in energy distributions form the basis of the concept of RBE. The RBE is defined as the ratio of the absorbed dose of referenced radiation to the absorbed dose of test radiation to produce the same level of biological effectiveness (ICRU 2003).

Biology of low LET radiation of a high dose rate and low energy

While low LET radiation has greater penetrance/lower energy deposition per unit depth than the high LET radiation, it is also important to remember that (for the low LET photons) lower energy photons penetrate tissues less deeply than their higher energy counterparts. Thus, while per photon energy of X-rays used for diagnostic procedures vs. “standard” therapeutic procedures is lower, these photons have a relatively disproportionate absorption in biological material (their penetration depth is smaller than that of higher energy X-rays). Brenner et al. (31) investigated the RBE of low energy, high dose rate low LET radiation. Using α/β ratio of 8 Gy for early responding endpoints, they determined that RBE could be considerably higher when compared to the “unit of the Cobalt”. Fowler et al. (32) studied this question on late responding tissues using α/β ratio of 3 Gy. He reported that RBE for X-ray photons for a given endpoint with 3 Gy α/β ratio should be 1.3. Considering the significant changes of this type of calculation when one uses different α/β ratios (i.e., 1 or 2 or 3) the limitations of this number cause serious concern. This work also “estimated” that the steep dose gradient associated with the penetration depth of low energy low LET radiation would lead to 10-20% changes in RBE with each 1-2 mm distance from the biological surface.

Radiation biological effectiveness (RBE) in a usual sense is defined as D/D treatment RFTX and is dependent on LET), cell survival level and treatment time. Kilovoltage X-ray (i.e., Intrabeam) has higher LET than megavoltage X-ray. For low energy X-ray photons regimen RBE decreases with depth due to beam hardening (i.e., the lowest energy photons get absorbed first, while higher energy photons within spectral range continue to traverse the tissue). On the contrary, for high dose, megavoltage X-rays regimens RBE increases with depth due to dose attestation (31).

It is estimated that external beam dose of 60 Gy given in 30 fractions at 2 Gy per fraction is equivalent to a single intraoperative radiotherapy fraction of 20-22 Gy (33) (considering α/β ratio of 10 Gy for acute reaction tissues). With the same formula when the tolerance of late responding tissues (α/β ratio of 3 Gy) is taken into consideration, the equivalent dose will be significantly higher. If we accept that L-Q model is reliable only for per fraction doses up to 6-8 Gy, and therefore might not be appropriate for modeling the effects of single high doses of 10-25 Gy such as are used for SBRT, we may even more “safely” conclude that using this formula is inappropriate for low energy radiation, which is commonly used intra-operatively [intraoperative radiotherapy (IORT)] and delivered as a high single dose (Table 3).

Table 3 Summary of biological effects
Full table

From the above table it is evident that almost none of the factors that underpin biological effects of “traditional” high dose rate radiotherapy apply either to application of hypofractioned high dose and high energy radiation (SBRT) or high dose low energy X-ray (IORT). Considering, furthermore that L-Q modeling and alpha beta calculations were developed for “traditional” radiotherapy, such modeling is inappropriate for either high dose, high energy (SBRT) or high dose, low energy radiation (IORT via Intrabeam). We agree with the new proposed hypothesis by Sperduto et al. (17) that inclusion of devascularization and indirect cell death in modeling of L-Q formality is necessary and would rekindle interest in this model, in spite of methodological difficulties for qualification of these factors. However, it is hard to think that while many factors make L-Q model inappropriate for clinical utility of SBRT and IORT, inclusion of one of the many factors isolated additional factors will make it appropriate. Also, we do agree that this is a new science, a new biology and much research on various biological aspects of these regiments remains to be done. In agreement with ref (17) the following research questions and ideas need to be investigated and experimentally/clinically verified in order for any model to be clinically useful. They include the following:

• Need for independent new radiation effects model(s) that would be confirmed in vivo, especially in humans;
• Different effect of SRS/SBRT (and possibly IORT) on hypoxic cells;
• Genetic and anti-vascular impact of new radiation on renal radiation;
• Impact of SBRT/SRS (and possibly IORT) on immune system (abscopal effect);
• The impact of devascularization by high dose per fraction on surrounding normal tissue (and possible related changes in OER);
• How and to what extent do the five Rs of classic radiobiology explain the results in SBRT and SRS (and possibly IORT) while one could argue (from above table) that there is no re-anything (17);
• In regards to dose delivery time, the delivery of 20 Gy in 20 minutes is not biologically equivalent to the same dose delivered in two hours. This needs to be verified clinically.

As mentioned before, the appropriate modeling of both tumor control and normal tissue toxicities in SRS, SBRT, and IORT requires application of new and emerging understanding of nuclear, cellular, and tissue level effects of high energy, high dose per fraction as well as high dose, low energy per fraction radiation.

As indicated by Kirkpatrick et al. (21) it is incumbent on our profession to generate meaningful pre-clinical and clinical experimental data on the effect of these new radiations on tumors and normal tissues in vivo, to develop models that reflect the true underlying mechanism governing the tumor control and impact normal tissues and to teach the next generation how to use and exploit these models in practice of clinical radiotherapy.

Acknowledgments

Funding: None.

Footnote

Provenance and Peer Review: This article was commissioned by the Guest Editors (Frank A. Giordano, Pedro Carlos Lara and Frederik Wenz) for the series “Intraoperative Radiotherapy II” published in Translational Cancer Research. The article has undergone external peer review.

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2015.04.06). The series “Intraoperative Radiotherapy II” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Fowler JF. 21 years of biologically effective dose. Br J Radiol 2010;83:554-68. [PubMed]
2. Brenner DJ, Hlatky LR, Hahnfeldt PJ, et al. The linear-quadratic model and most other common radiobiological models result in similar predictions of time-dose relationships. Radiat Res 1998;150:83-91. [PubMed]
3. Turesson I, Thames HD. Repair capacity and kinetics of human skin during fractionated radiotherapy: erythema, desquamation, and telangiectasia after 3 and 5 year's follow-up. Radiother Oncol 1989;15:169-88. [PubMed]
4. Bentzen SM, Christensen JJ, Overgaard J, et al. Some methodological problems in estimating radiobiological parameters from clinical data. Alpha/beta ratios and electron RBE for cutaneous reactions in patients treated with postmastectomy radiotherapy. Acta Oncol 1988;27:105-16. [PubMed]
5. Mc Bride WH, Withers HR. Biological bases of Radiation therapy in Principles & practice of Radiationtherapy. Halprom EC, Perez CA, Brady LW, et al. Sixth Edition. 2013:76.
6. Thames HD Jr, Withers R, Mason KA, et al. Dose-survival characteristics of mouse jejunal crypt cells. Int J Radiat Oncol Biol Phys 1981;7:1591-7. [PubMed]
7. Bentzen SM, Skoczylas JZ, Bernier J. Quantitative clinical radiobiology of early and late lung reactions. Int J Radiat Biol 2000;76:453-62. [PubMed]
8. Dubray B. Late complications of radiotherapy. Role of the time factor. Bull Cancer Radiother 1995;82:98-100. [PubMed]
9. Emami B, Lyman J, Brown A, et al. Tolerance of normal tissue to therapeutic irradiation. Int J Radiat Oncol Biol Phys 1991;21:109-22. [PubMed]
10. Withers HR. Radiation biology and treatment options in radiation oncology. Cancer Res 1999;59:1676s-84s. [PubMed]
11. Herskind C, Wenz F. Radiobiological comparison of hypofractionated accelerated partial-breast irradiation (APBI) and single-dose intraoperative radiotherapy (IORT) with 50-kV X-rays. Strahlenther Onkol 2010;186:444-51. [PubMed]
12. Fowler JF, Welsh JS, Howard SP. Loss of biological effect in prolonged fraction delivery. Int J Radiat Oncol Biol Phys 2004;59:242-9. [PubMed]
13. Park C, Papiez L, Zhang S, et al. Universal survival curve and single fraction equivalent dose: useful tools in understanding potency of ablative radiotherapy. Int J Radiat Oncol Biol Phys 2008;70:847-52. [PubMed]
14. Wennberg B, Lax I. The impact of fractionation in SBRT: analysis with the linear quadratic model and the universal survival curve model. Acta Oncol 2013;52:902-9. [PubMed]
15. Guerrero M, Li XA. Extending the linear-quadratic model for large fraction doses pertinent to stereotactic radiotherapy. Phys Med Biol 2004;49:4825-35. [PubMed]
16. Wang JZ, Huang Z, Lo SS, et al. A generalized linear-quadratic model for radiosurgery, stereotactic body radiation therapy, and high-dose rate brachytherapy. Sci Transl Med 2010;2:39ra48 [PubMed]
17. Sperduto PW, Song CW, Kirkpatrick JP, et al. A hypothesis: indirect cell death in the radiosurgery era. Int J Radiat Oncol Biol Phys 2015;91:11-3. [PubMed]
18. Coutard H. The results and methods of treatment of cancer by radiation. Ann Surg 1937;106:584-98. [PubMed]
19. Brown JM, Carlson DJ, Brenner DJ. The tumor radiobiology of SRS and SBRT: are more than the 5 Rs involved? Int J Radiat Oncol Biol Phys 2014;88:254-62. [PubMed]
20. Garcia LM, Wilkins DE, Raaphorst GP. Alpha/beta ratio: A dose range dependence study. Int J Radiat Oncol Biol Phys 2007;67:587-93. [PubMed]
21. Kirkpatrick JP, Meyer JJ, Marks LB. The linear-quadratic model is inappropriate to model high dose per fraction effects in radiosurgery. Semin Radiat Oncol 2008;18:240-3. [PubMed]
22. Park HJ, Griffin RJ, Hui S, et al. Radiation-induced vascular damage in tumors: implications of vascular damage in ablative hypofractionated radiotherapy (SBRT and SRS). Radiat Res 2012;177:311-27. [PubMed]
23. Song CW, Park H, Griffin RJ, et al. Radiobiology of stereotactic radiosurgery and stereotactic body radiation therapy. In: Levitt SH, Purdy JA, Perez CA, et al. eds. Technical Basis of Radiation Therapy, Medical Radiology. Radiation Oncology. Heidelberg, Berlin: Springer-Verlag, 2012:51-61.
24. Shibamoto Y, Otsuka S, Iwata H, et al. Radiobiological evaluation of the radiation dose as used in high-precision radiotherapy: effect of prolonged delivery time and applicability of the linear-quadratic model. J Radiat Res 2012;53:1-9. [PubMed]
25. Formenti SC, Demaria S. Systemic effects of local radiotherapy. Lancet Oncol 2009;10:718-26. [PubMed]
26. Formenti SC, Demaria S. Radiation therapy to convert the tumor into an in situ vaccine. Int J Radiat Oncol Biol Phys 2012;84:879-80. [PubMed]
27. Herskind C, Steil V, Kraus-Tiefenbacher U, et al. Radiobiological aspects of intraoperative radiotherapy (IORT) with isotropic low-energy X rays for early-stage breast cancer. Radiat Res 2005;163:208-15. [PubMed]
28. Rao SS, Oh JH, Jackson A, et al. Dose escalation, not “new biology,” can account for the efficacy of stereotactic body radiation therapy with non-small cell lung cancer. In regard to Brown et al. Int J Radiat Oncol Biol Phys 2014;89:692-3. [PubMed]
29. Liu Q, Schneider F, Ma L, et al. Relative Biologic Effectiveness (RBE) of 50 kV X-rays measured in a phantom for intraoperative tumor-bed irradiation. Int J Radiat Oncol Biol Phys 2013;85:1127-33. [PubMed]
30. Herskind C, Wenz F. Radiobiological aspects of intraoperative tumour-bed irradiation with low-energy X-rays (LEX-IORT). Transl Cancer Res 2014;3:3-17.
31. Brenner DJ, Leu CS, Beatty JF, et al. Clinical relative biological effectiveness of low-energy x-rays emitted by miniature x-ray devices. Phys Med Biol 1999;44:323-33. [PubMed]
32. Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol 1989;62:679-94. [PubMed]
33. Nag S, Tippin D, Grecula J, et al. Intraoperative high-dose-rate brachytherapy for paranasal sinus tumors. Int J Radiat Oncol Biol Phys 2004;58:155-60. [PubMed]